Signal to Noise Ration (SNR) is not an unknown terminology for Engineers and Tech professionals who are dealing with Digital or Analog form of Communication.Here we will explore the aspect of SNR in Optical Fiber Communication space known as Optical Signal to Noise Ratio(OSNR).
Warning! Keep patience while scrolling down to read as this article may seem long as this is important topic.Whole content is collected from free available trusted sources and can be downloaded or shared and covers content for everyone from beginner to professional so reader can absorb what he wants.Bingo! Let’s start it.
Some handy definition of OSNR to pick :-
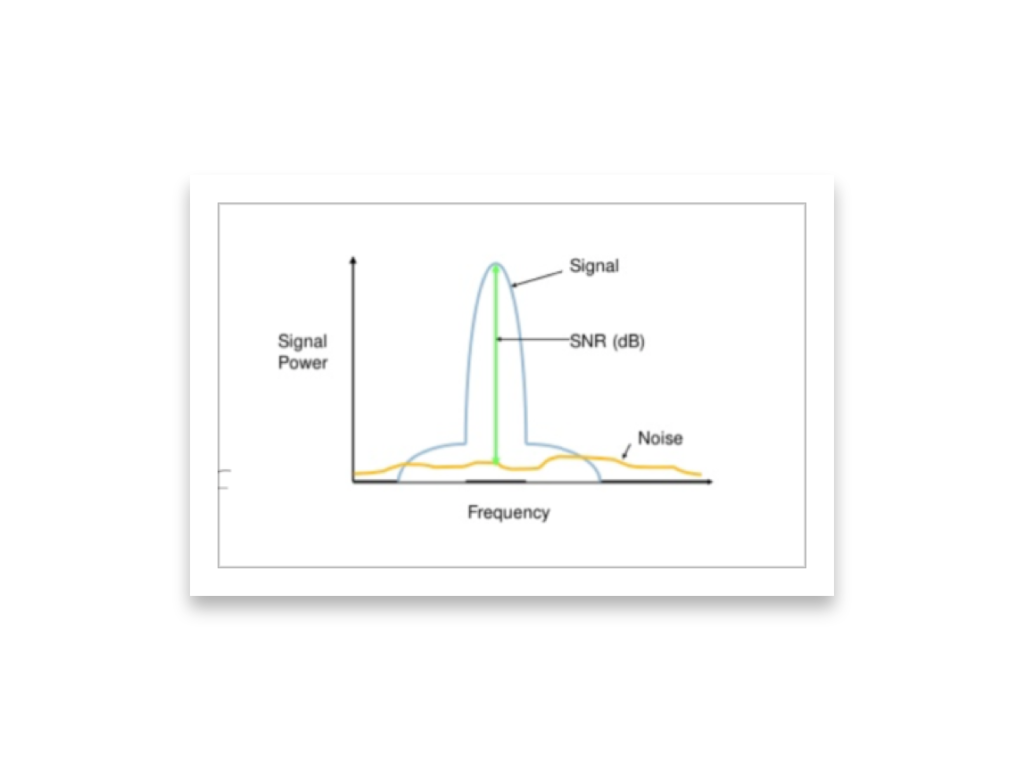
- OSNR [dB] is the measure of the ratio of signal power to noise power in an optical channel .
- OSNR is the short form of Optical Signal to Noise Ratio. It is key parameter to estimate performance of Optical Networks. It helps in BER calculation of Optical System.
- OSNR is important because it suggests a degree of impairment when the optical signal is carried by an optical transmission system that includes optical amplifiers.
- If we know the OSNR and the bandwidths, we can find Q and the BER
- It can be seen as the QoS at the physical layer of optical networks. OSNR is directly related to bit-error rate, which will lead to packet losses seen by higher layers.
- OSNR indirectly reflects BER and can provide a warning of potential BER deterioration.
- OSNR has long been recognised as a key performance indicator for amplified high-speed transmission networks to ensure network performance and reliability and it is related to many design parameter such as number or repeater/amplifiers ,reach ,available modulation formats etc.
- OSNR is a metric for the quality assessment of received signals that are corrupted by the ASE noise of EDFAs OSNR is defined as the ratio of the average optical signal power to the average optical noise power For a single EDFA with the output power Pout and the noise power NASE, OSNR is computed as
where
NF is the noise figure G is the amplifier gain
hf is the photon energy Δf is the optical measurement bandwidth
When addressing an OSNR value, it is important to define an optical reference bandwidth for the calculation of OSNR A bandwidth Δf of 12 5 GHz (or Δλ = 0 1 nm) is the typical reference bandwidth for calculating OSNR values
Now let’s explore it in more detail:-
Optical signal-to-noise ratio (OSNR) is used to quantify the degree of optical noise interference on optical signals. It is the ratio of service signal power to noise power within a valid bandwidth.When the signal is amplified by the optical amplifier (OA), like EDFA, its optical signal to noise ratio (OSNR) is reduced, and this is the primary reason to have limited number of OAs in a network.
The OSNR values that matter the most are at the receiver, because a low OSNR value means that the receiver will probably not detect or recover the signal. The OSNR limit is one of the key parameters that determine how far a wavelength can travel prior to regeneration.
OSNR serves as a benchmark indicator for the assessment of performance of optical transmission systems. DWDM networks need to operate above their OSNR limit to ensure error – free operation. There exists a direct relationship between OSNR and bit error rate (BER), where BER is the ultimate value to measure the quality of a transmission.
The value of OSNRout that is needed to meet the required system BER depends on many factors such as the bit rate, whether and what type of FEC is employed, the magnitude of any crosstalk or non-linear penalties in the DWDM line segments, etc.
Below picture highlights OSNR as one of the important parameter in a DWDM link.
Optical amplifiers such as erbium-doped fiber amplifiers (EDFAs) are normally employed in optical networks to compensate for the transmission losses over long distances. However, besides providing optical gain, EDFAs also add unwanted amplified spontaneous emission (ASE) noise into the optical signal. Furthermore, the cascading of EDFAs results in accumulation of ASE noise. ASE noise is typically quantified by OSNR and is one of the most important parameters to be monitored in optical networks since the BER is directly related to the signal OSNR Furthermore, it also plays a pivotal role in fault diagnosis and as a measure of general health of links in an optical network.
OSNR may change due to signal power changes or higher repeater noise levels due to aging.
Now lets read the Legacy method to measure it:-
The traditional method to measure OSNR is defined in the IEC 61280-2-9 standard and is known as the interpolation or out-of-band method, as shown in Figure-1 below
OSNR for a Point-to-Point Link
NFstage is the noise figure of the stage, h is Plank’s constant (6.6260 × 10-34), ν is the optical frequency 193 THz, and Δf is the bandwidth that measures the NF (it is usually 0.1 nm).
OSNR =158.9+ Pin.dBm −NF−10log(Br )
where
OSNRdB = optical signal to noise ratio of the optical amplifier, dB
Pin.dBm = average amplifier input signal power (DWDM systems use single-channel power), dBm
NF = amplifier noise figure, dB
h = Planck’s constant 6.626069 ◊ 10−34, Js
f = signal center frequency, Hz
Br = optical measurement bandwidth RBW, Hz
If the measurement optical bandwidth can be assumed to be 0.1 nm (12.48 GHz),
OSNR = 58 + Pin.dBm − NF
OSNRF.dB =158.9+Psource.dBm −Γ−NF−10log(Br)−10logN
where
OSNRF.dB = final OSNR seen at the receiver, dB
Psource.dBm = average source signal power into the first span(DWDM systems use single-channel power),dBm NF =amplifier noise figure, the same for all EDFAs, dB
Br = optical measurement bandwidth, Hz
N = number of amplifiers in the fiber link excluding the booster
Γ = span loss, the same for all spans, dB
Above equation provides the actual mathematical calculation of OSNR. This calculation method has quite a few approximations in which we can still find the system OSNR to a great degree of accuracy. In a multichannel WDM system, the design should consider OSNR for the worst channel (the one that has the worst impairment). The worst channel is generally the first or last channel in the spectrum.
we can see that the EDFA gain factor G is not considered. That is because OSNR is a ratio, and the gain acts equally on signal and noise, canceling the gain factor in the numerator and denominator. In other words, although EDFAs alleviate the upper bound on transmission length due to attenuation, by cascading EDFAs in a series, the OSNR is continuously degraded with transmission length and ASE (from EDFAs). This degradation can be lessened somewhat by distributed Raman amplifiers (DRAs).
Addition of Raman and OSNR change:-
As we can see from above equation the factor GRA in the numerator actually enhances the OSNR of the system.(stages) could be considered as EDFA hops here.
OSNR-based design essentially means whether the OSNR at the final stage (at the receiver) is in conformity with the OSNR that is desired to achieve the required BER. This also guarantees the BER requirement that is essential for generating revenue.
Below context is taken from article published by Jean-Sébastien
This method works well for networks up to 10G, without any Reconfigurable Optical Add-Drop Multiplexers (ROADM).
But traditional way of measurement don’t work anymore in High Speed Communications:-
However, IEC 61280-2-9 isn’t feasible for 100G+ signals as well as ROADM networks.
Figure 2 illustrates 100G channels spaced 50GHz apart, which is a common spacing in modern submarine (and terrestrial) networks. Polarization-Multiplexed (Pol-Mux) 100G+ signals are typically wider (require more optical spectrum) than legacy On-Off-Keyed (OOK) 10G signals, meaning they could overlap with neighboring channels. Accordingly, the midpoint between channels no longer consists only of noise, but rather of signal plus noise. Thus, the IEC method applied to 100G+ Pol-Mux signals will therefore lead to an overestimation of noise and inaccurate measurement date leading to incorrect decisions.
Figure 2: IEC 61280-2-9 Method Fails with Dense Pol-Mux 100G+ signals
Figure 3 illustrates a 100G signal that has gone through a ROADM, with the green area showing the channel bandwidth. Given filters inside a ROADM, the noise at the midpoint between channels will be carved (or filtered), leading to an underestimation of the noise level, if the IEC 61280-2-9 method is used, meaning this method is not feasible in ROADM-enabled coherent submarine networks.
Figure 3: IEC 61280-2-9 Method Fails in ROADM 100G+ Pol-Mux Networks
To address the issues described in Figures 2 and 3, in-band OSNR was introduced around 2009 to support OSNR measurements of 10G signals in ROADM networks and 40G OOK signals. However, this method can’t be applied to coherent, Pol-Mux 100G+ signals, because of technical reasons beyond the scope of this blog. Consequently, Pol-Mux OSNR techniques have been introduced to support 100G+ signals, which is the topic of the latest standards.
Appropriate standards for Pol-Mux OSNR measurements?
There are two standards providing relevant guidelines for OSNR measurements of Pol-Mux signals. They are the China Communications Standards Association (CCSA) YD/T 2147-2010 standard and the IEC 61282-12 standards, which was recently introduced in February 2016. Both standards provide a future-proof definition of OSNR, which can be applied to any type of signal, at any data rate, including super-channels and flexible-grid signals. Specifically, the IEC-61282-12 standard specifies that:
where:
- s(λ) is the time-averaged signal spectral power density, not including ASE, expressed in W/nm
- ρ(λ) is the ASE spectral power density, independent of polarization, expressed in W/nm
- Br is the reference bandwidth expressed in nm (usually 0.1nm if not otherwise stated)
- and the integration range in nm from λ1to λ2is chosen to include the total signal spectrum
The only drawback of these two standards is that a careful application of their formulae requires turning off channels, to access the Amplified Spontaneous Emission (ASE) noise floor, which isn’t possible on an in-service lest we upset end-users! Fortunately, in-service Pol-Mux OSNR methods have been introduced.
below table summarizes the correct OSNR method for each type of signal.
| Data Rate | ROADM Present? | OSNR Method | Works on in-service network? |
| ≤10G signals | No | IEC 61280-2-9 | Yes |
| ≤10G signals | Yes | In-band OSNR | Yes |
| Non-coherent 40G signals | Yes or No | In-band OSNR | Yes |
| Coherent 100G+ signals | Yes or No | Pol-Mux OSNR (IEC and CCSA standards) | No |
| Coherent 100G+ Signals | Yes or No | In-Service Pol-Mux OSNR | Yes |
Table 1: OSNR Measurement Methods for Various Signal Types
Using the wrong OSNR measurement method for a given signal can have a significant impact on results, as it can lead to errors ranging from a few dBs up to 10dB, potentially leading to future outages. Using the proper method guarantees the right OSNR measurements are achieved leading to accurate network modeling, link simulation, and maintenance of ongoing submarine cable network performance.
Summarizing the importance of OSNR and its proper measurement method?
Some of the benefits of OSNR testing, including avoiding network outages, optimizing troubleshooting times, and ensuring optimal terrestrial and submarine cable performance. OSNR will become even more critical at data rates beyond 100G, because of the more stringent OSNR thresholds that will be required. Several OSNR methods have been introduced over the years, so the key takeaway is that the right OSNR measurement method must be used on a specific signal type to get accurate results.
Introduction to OSNR for high speed communication
The OSNR is the signal-to-noise ratio (SNR) measured in a reference optical bandwidth, where frequently a bandwidth Bref of 12.5 GHz is used corresponding to 0.1 nm wavelength. The OSNR relates to the Es ∕N0 and Eb ∕N0 as
where Bref is the previously introduced reference bandwidth, RS corresponds to the symbol rate of the transmission, r is the mentioned rate of the code with r = k∕n, and q corresponds to the number of bits mapped to each modulation symbol.
The use of high-order modulation formats requires a higher optical signal-to-noise ratio (OSNR), which may result in a significantly reduced achievable transmission distance .Following diagram shows the OSNR estimation stage for High Speed Optical Communication.
Lets talk about OSNR Penalty now:-
OSNR penalty is obtained from the BER curves and determined at a particular BER. A value of the OSNR penalty is obtained by comparing the values of OSNR before and after the change of the parameters, which are under test, as given by
OSNRpenalties = various transmission penalties due to CD, PMD, PDL, etc. (note these penalties maybe different for 100G vs. 400G)
Calculation of Q-Factor from OSNR
The OSNR is the most important parameter that is associated with a given optical signal. It is a measurable (practical) quantity for a given network, and it can be calculated from the given system parameters. The following sections show you how to calculate OSNR. This section discusses the relationship of OSNR to the Q-factor.
The logarithmic value of Q (in dB) is related to the OSNR
In the equation, B0 is the optical bandwidth of the end device (photodetector) and Bc is the electrical bandwidth of the receiver filter.
Q is somewhat proportional to the OSNR
BER FORMULAS FOR THE MOST COMMON QAM SYSTEMS
Gray coding is assumed for all formats. For PM-BPSK the exact formula is:
For PM-QPSK the exact formula is:
For PM-16QAM and PM-64QAM, respectively, the following formulas are approximate, but their accuracy is better than ±0.05 dB of OSNRNL over the range 10−1 and 10−4:
EDFA Noise – Why Input Power Matters
Optical signal suffers more than only attenuation. In amplitude, spectrally, temporally signal interaction with light- matter, light- light, light-matter-light leads to other signal disturbances
such as :-
- Power reduction
- Dispersion
- Polarization
- Unbalanced amplification
Thus leading to random noise, which causes misalignments, jitter and other disturbances resulting in erroneous bits, the rate of which is known as bit-error-rate
Because of all possible influences outlined bits transmitted by source and bits arriving at the receiver may not have the same value. In actuality a threshold value is set at the receiver, above the threshold refers to a logic “one” and below threshold refers to a logic “zero”.
In order to measure BER in photonic regime, the optical signal is converted to electrical signal.
Example: Assuming a confidence level of 99%, BER threshold set at 10-10 and a bit rate of 2.5 Gb/s the required number n is 6.64 x 1010
Given the OSNR, the empirical formula to calculate BER for single fiber is
Log10 (BER) = 10.7-1.45 (OSNR)
Some mathematical aspects of OSNR:-
Assume that OSNR = 14.5 dB
ThenLog10 (BER) = 10.7-1.45 (14.5) = -10.30
Therefore BER = 10(-10.30) BER is approx 10- 10
In an experimental environment where factors such as loss, dispersion, and non-linear effects are excluded, if the OSNR is less than the specified threshold, the pre-FEC BER will be excessively large and uncorrectable bit errors will be generated. The OSNR threshold in this case is called B2B OSNR tolerance.
Calculating OSNR from OSA:
As can be seen from the definitions above, two quantities must be known to compute OSNR: the Total Signal Power, and the amount of ASE Noise Power present in a 0.1nm bandwidth.
Measuring the ASE power:
When the ASE noise floor is clearly visible left and right of the optical signal, the ASE Noise Power at the signal wavelength can be interpolated from two measurements made left and right of the signal.
Note that power values are frequently provided in dBm by the OSA – whether the measurements is made using integrated power function or a user-specified resolution bandwidth. To convert the values in dBm to mW, the following relation must be used:
Measuring the Total Signal Power:
When making this measurement it is important to use a bandwidth that is large enough to capture the entire signal:
Note that when measuring a DWDM spectrum, the power of each DWDM signal cannot be measured independent of ASE noise present in the measurement bandwidth.
Ie., the value that is actually measured is: Total Signal Power + ASE Noise Power.
To get the Total Signal Power only, the ASE noise content (measured separately in the previous step) must be subtracted from the measurement. Since the measurement bandwidth used to measure the noise on its own (ASE BW) may be different from the bandwidth used to measure the signal (Signal BW), a factor is added to the equation. This removes the correct amount of noise from the measurement.
where:
Signal BW is the bandwidth used to measured the signal,
ASE BW is the bandwidth used to measure the ASE Noise Power only (e.g., 0.1nm).
Calculating OSNR from measurements:
Since OSNR must be reported as signal power with respect to 0.1nm worth of ASE noise, the denominator of the OSNR equation also includes a factor. This adjusts the amount of ASE noise measured to an amount expected inside a 0.1nm bandwidth:
Thus
In a transmission chain, the relative evolution of the optical signal and noise levels is usually characterized by the optical signal-to-noise ratio (OSNR). The OSNR, in a given optical bandwidth, is defined as
Accordingly with the fluctuation dissipation theorem, it also adds noise, making its output OSNR lower than its input one. This OSNR degradation is expressed in terms of noise factor (NF) defined as:
where G is the optical power gain (or the attenuation coefficient) of the device which is larger (or smaller) than 1. NF is denoted noise figure when it is expressed in dB. Because the relative importance of the added noise strongly depends on the input noise level, NF is only an intrinsic parameter of the optical device (i.e. independent of the input signal and noise) when an input reference noise is defined.
For polarization insensitive devices, input noise and output noise usually do depend on polarization, making noise figure independent of polarization considerations.
Single amplifier noise factor
OSNR at the output of an optical amplifier with an output power Pout and for an optical bandwidth B0 is expressed as:
where m=1 or 2 is the number of polarization modes contributing to noise. It is usual to consider the two polarization modes (m=2) of the noise and to make reference to an optical bandwidth equal to 0.1 nm corresponding to Bo = 12.5GHz at a wavelength of 1550 nm. In this particular situation, the OSNR is expressed in dB as:
NFdB, Noise factor of a cascade of fibers and amplifiers
Let us consider now the cascade of spans displayed in Figure and including Namp optical fiber spans with an attenuation coefficient A and Namp lumped linear phase insensitive amplifiers with a gain net G and a noise factor NF. For each span a near compensation of the signal attenuation by the gain is assumed, making its net gain GSPAN 5 GA close to 1. Each fiber reduces the sig- nal level and reduces the noise level nearly in the same way. Since the input noise level is far above the appropriated reference level, the attenuation noise of the fiber is negligible and the OSNR is kept nearly unchanged. Each amplifier output POUT restores the input noise of the link but adds the amplifier noise.
The accumulated noise is Namp times larger than single amplifier and we have:
To bridge transoceanic distances while keeping a high OSNR (optical SNR), it is crucial to limit the noise contribution added by the successive amplifiers. The impact of the added noise on the output OSNR can be calculated with:
This equation can also be expressed in a more physical manner:
where N is the amplifier count, and Δλ the width of the filter where the OSNR is expressed. The number “30” at the end of Equation corresponds to the conversion of signal input power from units in watts into units scaled in milliwatts.
Few Key Concepts to remember
The OSNR values that matter the most are at the receiver, because a low OSNR value means that the receiver will probably not detect or recover the signal.
The OSNR limit is one of the key parameters that determine how far a wavelength can travel prior to regeneration.
OSNR serves as a benchmark indicator for the assessment of performance of optical transmission systems. DWDM networks need to operate above their OSNR limit to ensure error – free operation.
There exists a direct relationship between OSNR and bit error rate (BER), where BER is the ultimate value to measure the quality of a transmission. Given the OSNR, the empirical formula to calculate BER for single fiber is:
Log10 (BER) = 10.7-1.45 (OSNR)
In DWDM links a rule of thumb would be to target an OSNR value greater than 15 dB to 18 dB at the receiver.
OSNR requirements depend on:
- Location: The required OSNR will be different for different locations in the light path. The OSNR requirement will be higher closer to the transmitter and lower closer to the receiver. This is because optical amplifiers and reconfigurable add/drop modules (ROADMs) add noise, which means that the OSNR value degrades after going through each optical amplifier or ROADM. To ensure that the OSNR value is high enough for proper detection at the receiver, the number of optical amplifiers and ROADMs needs to be considered when designing a network.
- Type of Network: For a metro network, an OSNR value of >40 dB at the transmitter might be perfectly acceptable, because there are not many amps between the transmitter and the receiver.For a submarine network, the OSNR requirements at the transmitter are much higher.
-
-
-
-
-
-
- Data Rate: With the increase in the data rate for a specific modulation format, the OSNR requirement also increases.
- Target BER: A lower target BER calls for a higher OSNR value.
-
-
-
-
-
-
The exact requirements at the receiver will vary from one manufacturer to another. Table displays a few average OSNR figures to guarantee a BER lower than 10-8 at the receiver
Note: Now try to utilise the above concepts and equations whatever way you want .