Noise figure (NF) is a critical parameter in optical amplifiers that quantifies the degradation of signal-to-noise ratio during amplification. In multi-span optical networks, the accumulated noise from cascaded amplifiers ultimately determines system reach, capacity, and performance.
While amplifiers provide the necessary gain to overcome fiber losses, they inevitably add amplified spontaneous emission (ASE) noise to the signal. The noise contribution from each amplifier accumulates along the transmission path, with early-stage amplifiers having the most significant impact on the end-to-end system performance.
Understanding the noise behavior in cascaded amplifier chains is fundamental to optical network design. This article explores noise figure fundamentals, calculation methods, and the cumulative effects in multi-span networks, providing practical design guidelines for optimizing system performance.
Definition and Physical Meaning
Noise figure is defined as the ratio of the input signal-to-noise ratio (SNR) to the output SNR of an amplifier, expressed in decibels (dB):
NF = 10 log₁₀(SNRin / SNRout) dB
Alternatively, it can be expressed using the noise factor F (linear scale):
NF = 10 log₁₀(F) dB
In optical amplifiers, the primary noise source is amplified spontaneous emission (ASE), which originates from spontaneous transitions in the excited gain medium. Instead of being stimulated by the input signal, these transitions occur randomly and produce photons with random phase and direction.
Quantum Limit and Physical Interpretation
Even a theoretically perfect amplifier has a quantum-limited minimum noise figure of 3dB. This fundamental limit exists because the amplification process inherently introduces at least half a photon of noise per mode.
The noise figure is related to several physical parameters:
- Spontaneous Emission Factor (nsp): Represents the quality of population inversion in the active medium
- Population Inversion: The ratio of atoms in excited states versus ground states
- Quantum Efficiency: How efficiently pump power creates population inversion
NF = 2·nsp·(1-1/G)
As gain (G) becomes large, this approaches: NF = 2·nsp, with a theoretical minimum of 3dB when nsp = 1.
Factors Affecting Noise Figure
Gain and Population Inversion
The population inversion level directly affects the noise figure. Higher inversion leads to lower ASE and therefore lower noise figure. Key relationships include:
- Gain Level: Higher gain typically results in better inversion and lower NF up to a saturation point
- Pump Power: Increased pump power improves inversion up to a saturation level
- Gain Medium Length: Longer gain medium increases available gain but can increase NF if inversion is not maintained throughout
Input Power Dependence
Noise figure varies with input signal power:
- At very low input powers, the gain can be higher but the effective NF may increase due to insufficient saturation
- At high input powers, gain saturation occurs, leading to a higher effective NF
- The optimal input power range for lowest NF is typically 10-15dB below the saturation input power
Wavelength Dependence
Noise figure typically varies across the operating wavelength band:
- The wavelength dependence follows the gain spectrum of the amplifier
- In typical optical amplifiers, NF is often lowest near the peak gain wavelength
- Edge wavelengths generally experience higher NF due to lower inversion and gain
- This wavelength dependence can impact system design, especially for wideband applications
Temperature Effects
Temperature significantly impacts noise figure performance:
- Higher temperatures typically increase NF due to reduced population inversion efficiency
- Temperature-dependent cross-sections in the gain medium affect both gain and noise performance
- Thermal management is critical for maintaining consistent NF performance, especially in high-power amplifiers
EDFA Specifications
In optical networks, various EDFA designs are available with specific noise figure performance characteristics:
| Application | Typical NF Range | Typical Gain Range |
|---|---|---|
| Metro access | 6.0-7.0dB | 12-21dB |
| Metro/regional | 5.5-6.5dB | 14-22dB |
| Regional with mid-stage access | 5.5-7.5dB | 15-28dB |
| Long-haul with mid-stage access | 5.0-7.0dB | 25-37dB |
| Regional single-stage | 5.0-6.0dB | 15-28dB |
| Long-haul single-stage | 5.0-6.0dB | 25-37dB |
| Ultra-short span booster | 15.0-17.0dB | 5-7dB |
Temperature Sensitivity
Noise figure is temperature sensitive, with performance typically degrading at higher temperatures due to:
- Reduced pump efficiency
- Changes in population inversion
- Increased thermal noise contributions
Most optical amplifiers are designed to operate in accordance with standard telecom environmental specifications like ETS 300 019-1-3 Class 3.1E for environmental endurance.
Cascaded Amplifiers and Noise Accumulation
In optical networks, signals typically pass through multiple amplifiers as they traverse through fiber spans. Understanding how noise accumulates in these multi-span systems is critical for designing networks that meet performance requirements.
Friis' Formula and Cascaded Amplifier Systems
The noise accumulation in a chain of optical amplifiers follows Friis' formula, which was originally developed for electronic amplifiers but applies equally to optical systems:
Ftotal = F1 + (F2-1)/G1 + (F3-1)/(G1·G2) + ... + (Fn-1)/(G1·G2···Gn-1)
Where:
- Ftotal is the total noise factor (linear, not in dB)
- Fi is the noise factor of the i-th amplifier
- Gi is the gain (linear) of the i-th amplifier
In optical systems, this formula must account for span losses between amplifiers:
Ftotal = F1 + (L1·F2-1)/G1 + (L1·L2·F3-1)/(G1·G2) + ...
Where Li represents the span loss (linear) between amplifiers i and i+1.
Key Insights from Friis' Formula
The most significant insight from Friis' formula is that the first amplifier has the most substantial impact on the overall noise performance. Each subsequent amplifier's noise contribution is reduced by the gain of all preceding amplifiers.
Practical implications include:
- Always use the lowest noise figure amplifier at the beginning of a chain
- The impact of noise figure improvements diminishes for amplifiers later in the chain
- Pre-amplifiers are more critical for noise performance than boosters
- Mid-stage components (like DCFs) should have minimal loss to preserve good noise performance
OSNR Evolution in Multi-span Systems
The optical signal-to-noise ratio (OSNR) evolution through a multi-span system can be approximated by:
OSNRdB ≈ Plaunch - α·L - NF - 10·log10(N) - 10·log10(Bref) + 58
Where:
- Plaunch is the launch power per channel (dBm)
- α is the fiber attenuation coefficient (dB/km)
- L is the span length (km)
- NF is the amplifier noise figure (dB)
- N is the number of spans
- Bref is the reference bandwidth for OSNR measurement (typically 0.1nm)
- 58 is a constant that accounts for physical constants (h𝜈)
The key insight from this equation is that OSNR degrades by 3dB each time the number of spans doubles (10·log10(N) term). This creates a fundamental limit to transmission distance in amplified systems.
Practical Example: OSNR Calculation in a Multi-span System
Consider a 10-span system with the following parameters:
- Launch power: +1dBm per channel
- Span length: 80km
- Fiber loss: 0.2dB/km (total span loss = 16dB)
- Amplifier gain: 16dB (exactly compensating span loss)
- Amplifier noise figure: 5dB
- Reference bandwidth: 0.1nm (~12.5GHz at 1550nm)
Step 1: Calculate the OSNR for a single span:
OSNR1-span = +1 - 16 - 5 - 10·log10(1) - 10·log10(12.5) + 58
= +1 - 16 - 5 - 0 - 11 + 58 = 27dB
Step 2: Calculate the OSNR degradation due to multiple spans:
OSNR degradation = 10·log10(N) = 10·log10(10) = 10dB
Step 3: Calculate the final OSNR:
OSNR10-spans = OSNR1-span - 10·log10(N) = 27 - 10 = 17dB
With a typical OSNR requirement of 12-15dB for modern coherent transmission formats, this system has adequate margin for reliable operation. However, extending to 20 spans would reduce OSNR by another 3dB to 14dB, approaching the limit for reliable operation.
Multi-Stage Amplifier Design
Based on the principles of Friis' formula, multi-stage amplifiers with optimal noise performance typically follow a design where:
Key design principles include:
- Low-Noise First Stage: The first stage should be optimized for low noise figure, even at the expense of output power capability
- Power-Optimized Second Stage: The second stage can focus on power handling and efficiency once the SNR has been established by the first stage
- Minimal Mid-Stage Loss: Any passive components (filters, isolators, etc.) between stages should have minimal insertion loss to avoid degrading the noise performance
EDFA Models and Cascaded Performance
Various types of optical amplifiers are designed with cascaded performance in mind:
| Type | Mid-Stage Features | Design Optimization |
|---|---|---|
| Variable gain with mid-stage access | Mid-stage access for DCF | Optimized for regional networks |
| High-gain variable gain with mid-stage access | Mid-stage access for DCF | Optimized for high-gain applications |
| Variable gain with mid-stage access and C/T filters |
Mid-stage access for DCF | Optimized for high-power applications with OSC handling |
Typical mid-stage dispersion compensation fiber (DCF) parameters tracked in optical networks include dispersion value, PMD, and tilt, which are critical for maintaining overall system performance.
Automatic Laser Shutdown (ALS) and Safety
In high-power multi-span systems, safety mechanisms like Automatic Laser Shutdown (ALS) are implemented to prevent hazardous conditions during fiber breaks or disconnections:
- ALS triggers when LOS (Loss Of Signal) is detected on a line port
- During ALS, EDFAs are disabled except for periodic 30-second probing intervals at reduced power (20dBm)
- Normal operation resumes only after signal restoration for at least 40 seconds
Modern optical amplifiers feature ALS functionality with configurable parameters to ensure both optimal performance and safety in cascaded environments.
Network Applications and Optimization Strategies for Optical Amplifiers
Different segments of optical networks have varying requirements for noise figure performance based on their application, reach requirements, and economic considerations.
Network Segment Requirements
Access Networks
Access networks are generally tolerant of higher noise figures (6-7dB) because:
- They involve fewer amplifiers in cascade
- They often operate with higher channel powers
- Transmission distances are relatively short
- Cost sensitivity is higher than performance optimization
Metro/Regional Networks
Metro and regional networks require balanced NF performance (5-6dB) with:
- Good dynamic range to handle varying traffic patterns
- Flexibility to support different node configurations
- Moderate reach capabilities (typically 4-10 spans)
- Reasonable cost-performance trade-offs
Long-haul Networks
Long-haul and submarine networks demand optimized low-NF designs (4-5dB) due to:
- Large number of amplifiers in cascade (often 10-20+)
- Need to maximize reach without electrical regeneration
- Requirement to support advanced modulation formats
- Justification for premium components due to overall system economics
Economic Implications of Noise Figure
Improving noise figure comes with cost implications that must be carefully evaluated:
| NF Improvement | Typical Cost Increase | Performance Benefit | Economic Justification |
|---|---|---|---|
| 6.0dB → 5.5dB | +5-10% | ~10% reach increase | Generally cost-effective |
| 5.5dB → 5.0dB | +10-15% | ~10% reach increase | Often justified for long-haul |
| 5.0dB → 4.5dB | +15-25% | ~10% reach increase | Specialty applications only |
| 4.5dB → 4.0dB | +30-50% | ~10% reach increase | Rarely justified economically |
The economic tradeoffs include:
- Capital vs. Operating Expenses: Higher-quality, lower-NF amplifiers cost more initially but may reduce the need for additional amplifier sites and regeneration points
- Upgrade Paths: Better NF provides margin for future capacity upgrades with more advanced modulation formats
- Lifecycle Considerations: Premium amplifiers may maintain better performance over their operational lifetime, delaying replacement needs
- System Capacity: Improved NF can enable higher capacity through better OSNR margin, often at lower cost than adding new fiber routes
Operational Optimization Strategies
For system operators using EDFAs, several practical optimization strategies can help maximize performance:
1. Gain Optimization
Modern optical amplifiers support different operation modes with specific gain management approaches:
- Automatic Mode: Maintains output power per channel based on saturation power and maximum channel count settings
- Semi-automatic Mode: Maintains a fixed output power per channel
- Constant Gain Mode: Maintains a fixed gain regardless of input power variations
- Automatic Power Control (APC) Mode: Provides automatic power control for specialized applications
- Automatic Current Control (ACC) Mode: Provides precise pump current control for specialized applications
Advanced amplifiers implement specific algorithms for gain control that include careful monitoring of required gain versus actual gain, with alarms for out-of-range or out-of-margin conditions.
2. Tilt Management
Spectral tilt management is crucial for maintaining consistent OSNR across all channels:
- Modern EDFAs automatically adjust tilt to compensate for fiber and component tilt
- SRS (Stimulated Raman Scattering) tilt compensation is included for high-power systems
- Built-in tilt values are stored in amplifier memory and used as reference points
- For ultra-short span boosters and extended C-band amplifiers, specialized tilt algorithms account for fiber type
3. Temperature Control
Optical amplifiers typically specify operational temperature ranges in accordance with telecom standards like ETS 300 019-1-3 Class 3.1E, emphasizing the importance of controlling environmental conditions to maintain optimal performance.
4. Fiber Plant Optimization
Several fiber plant parameters impact noise figure performance:
- Span Loss: Monitored and alarmed when outside expected range
- Mid-stage Loss: For dual-stage amplifiers, carefully managed for optimal performance
- Transmission Fiber Type: Configuration option that affects SRS tilt compensation
- DCF Parameters: Dispersion, PMD, and tilt tracked in network control protocols
Noise Figure Design Guidelines
- Place Highest Quality First: Always use the lowest noise figure amplifiers at the beginning of the chain where they have the most impact
- Budget Wisely: Budget 0.5-1.0dB extra margin for each amplifier to account for aging and temperature variations over the system lifetime
- Consider Total Cost: Evaluate the total cost impact of NF improvements, including reduced regeneration needs and extended reach capabilities
- Monitor Trends: Establish baseline NF measurements and monitor for gradual degradation that might indicate pump laser aging
- Balance Requirements: Balance NF with other parameters like output power, gain flatness, and dynamic range based on specific application needs
- Test Under Load: Validate NF performance under realistic channel loading conditions, not just with a single test wavelength
Future Trends in Noise Figure Technology
Emerging technologies for noise figure optimization include:
- AI-Driven Optimization: Machine learning algorithms that dynamically adjust amplifier parameters based on real-time network conditions
- Advanced Material Science: New dopant materials and glass compositions that enable better population inversion and reduced spontaneous emission
- Integrated Photonics: Silicon photonics and other integrated platforms that combine amplification with filtering and control functions
- Quantum-Enhanced Amplification: Phase-sensitive amplification and other quantum approaches that can theoretically break the 3dB quantum noise limit
- Distributed Intelligence: Network-wide optimization that coordinates multiple amplifiers for global noise minimization
EDFA Implementation Examples
Metro Network Design
A typical metro network implementation might include:
- Terminal nodes using fixed-gain boosters and pre-amplifiers
- FOADM nodes using low-gain pre-amplifiers
- Flexible OADM nodes employing medium-gain boosters
Regional Network Design
For regional networks, typical designs include:
- Terminal nodes with AWG Mux/DeMux and EDFAs for amplification
- Modern terminals with WSS for automatic equalization
- ROADM nodes employing pre-amplifiers with mid-stage access for DCF compensation and boosters
- In-line amplifier nodes (ILAN) using EDFAs to compensate for transmission fiber and DCF loss
Specialized Applications
Some specialized EDFA designs address unique requirements:
- Ultra-short span boosters: Very high output power (26dBm) with narrow gain range (5-7dB)
- High-power pre-amps: For ROADM applications with specialized eye-safety verification process
- Pluggable EDFAs: For applications requiring compact, modular amplification in form factors like CFP2
Conclusion
Noise figure is a fundamental parameter that sets ultimate performance limits for optical amplifier systems. Modern EDFA families demonstrate a comprehensive approach to addressing various network requirements with optimized designs for different applications.
Key takeaways include:
- Noise figure quantifies an amplifier's SNR degradation, with a quantum-limited minimum of 3dB
- In cascaded configurations, noise accumulates according to Friis' formula, with early-stage amplifiers having the most significant impact
- Network operators can optimize NF through proper pump power settings, gain optimization, temperature control, and careful wavelength planning
- Multi-stage designs with low-NF first stages offer the best overall performance for critical applications
- Economic considerations must balance the additional cost of lower-NF amplifiers against improved system reach and capacity
The evolution of EDFA technology reflects the ongoing refinement of noise figure optimization techniques, with newer designs and features continually addressing the evolving requirements of optical networks.
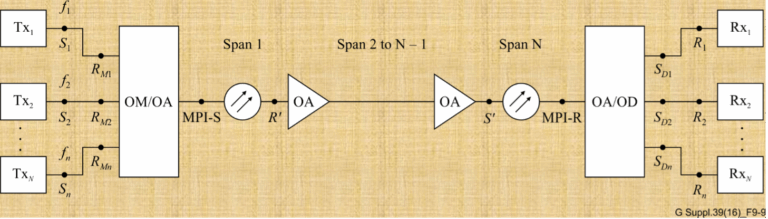
Optical networks are the backbone of the internet, carrying vast amounts of data over great distances at the speed of light. However, maintaining signal quality over long fiber runs is a challenge due to a phenomenon known as noise concatenation. Let’s delve into how amplified spontaneous emission (ASE) noise affects Optical Signal-to-Noise Ratio (OSNR) and the performance of optical amplifier chains.
The Challenge of ASE Noise
ASE noise is an inherent byproduct of optical amplification, generated by the spontaneous emission of photons within an optical amplifier. As an optical signal traverses through a chain of amplifiers, ASE noise accumulates, degrading the OSNR with each subsequent amplifier in the chain. This degradation is a crucial consideration in designing long-haul optical transmission systems.
Understanding OSNR
OSNR measures the ratio of signal power to ASE noise power and is a critical parameter for assessing the performance of optical amplifiers. A high OSNR indicates a clean signal with low noise levels, which is vital for ensuring data integrity.
Reference System for OSNR Estimation
As depicted in Figure below), a typical multichannel N span system includes a booster amplifier, N−1 line amplifiers, and a preamplifier. To simplify the estimation of OSNR at the receiver’s input, we make a few assumptions:
- All optical amplifiers, including the booster and preamplifier, have the same noise figure.
- The losses of all spans are equal, and thus, the gain of the line amplifiers compensates exactly for the loss.
- The output powers of the booster and line amplifiers are identical.
Estimating OSNR in a Cascaded System
E1: Master Equation For OSNR
Pout is the output power (per channel) of the booster and line amplifiers in dBm, L is the span loss in dB (which is assumed to be equal to the gain of the line amplifiers), GBA is the gain of the optical booster amplifier in dB, NFis the signal-spontaneous noise figure of the optical amplifier in dB, h is Planck’s constant (in mJ·s to be consistent with Pout in dBm), ν is the optical frequency in Hz, νr is the reference bandwidth in Hz (corresponding to c/Br ), N–1 is the total number of line amplifiers.
The OSNR at the receivers can be approximated by considering the output power of the amplifiers, the span loss, the gain of the optical booster amplifier, and the noise figure of the amplifiers. Using constants such as Planck’s constant and the optical frequency, we can derive an equation that sums the ASE noise contributions from all N+1 amplifiers in the chain.
Simplifying the Equation
Under certain conditions, the OSNR equation can be simplified. If the booster amplifier’s gain is similar to that of the line amplifiers, or if the span loss greatly exceeds the booster gain, the equation can be modified to reflect these scenarios. These simplifications help network designers estimate OSNR without complex calculations.
1) If the gain of the booster amplifier is approximately the same as that of the line amplifiers, i.e., GBA » L, above Equation E1 can be simplified to:
E1-1
2) The ASE noise from the booster amplifier can be ignored only if the span loss L (resp. the gain of the line amplifier) is much greater than the booster gain GBA. In this case Equation E1-1 can be simplified to:
E1-2
3) Equation E1-1 is also valid in the case of a single span with only a booster amplifier, e.g., short‑haul multichannel IrDI in Figure 5-5 of [ITU-T G.959.1], in which case it can be modified to:
E1-3
4) In case of a single span with only a preamplifier, Equation E1 can be modified to:
Practical Implications for Network Design
Understanding the accumulation of ASE noise and its impact on OSNR is crucial for designing reliable optical networks. It informs decisions on amplifier placement, the necessity of signal regeneration, and the overall system architecture. For instance, in a system where the span loss is significantly high, the impact of the booster amplifier on ASE noise may be negligible, allowing for a different design approach.
Conclusion
Noise concatenation is a critical factor in the design and operation of optical networks. By accurately estimating and managing OSNR, network operators can ensure signal quality, minimize error rates, and extend the reach of their optical networks.
In a landscape where data demands are ever-increasing, mastering the intricacies of noise concatenation and OSNR is essential for anyone involved in the design and deployment of optical communication systems.
References
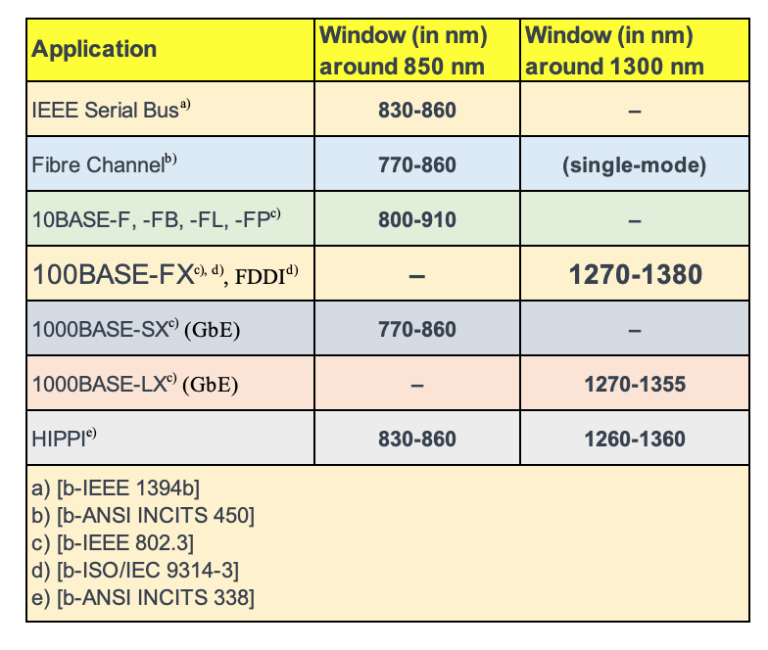
While single-mode fibers have been the mainstay for long-haul telecommunications, multimode fibers hold their own, especially in applications where short distance and high bandwidth are critical. Unlike their single-mode counterparts, multimode fibers are not restricted by cut-off wavelength considerations, offering unique advantages.
The Nature of Multimode Fibers
Multimode fibers, characterized by a larger core diameter compared to single-mode fibers, allow multiple light modes to propagate simultaneously. This results in modal dispersion, which can limit the distance over which the fiber can operate without significant signal degradation. However, multimode fibers exhibit greater tolerance to bending effects and typically showcase higher attenuation coefficients.
Wavelength Windows for Multimode Applications
Multimode fibers shine in certain “windows,” or wavelength ranges, which are optimized for specific applications and classifications. These windows are where the fiber performs best in terms of attenuation and bandwidth.
IEEE Serial Bus (around 850 nm): Typically used in consumer electronics, the 830-860 nm window is optimal for IEEE 1394 (FireWire) connections, offering high-speed data transfer over relatively short distances.
Fiber Channel (around 770-860 nm): For high-speed data transfer networks, such as those used in storage area networks (SANs), the 770-860 nm window is often used, although it’s worth noting that some applications may use single-mode fibers.
Ethernet Variants:
- 10BASE (800-910 nm): These standards define Ethernet implementations for local area networks, with 10BASE-F, -FB, -FL, and -FP operating within the 800-910 nm range.
- 100BASE-FX (1270-1380 nm) and FDDI (Fiber Distributed Data Interface): Designed for local area networks, they utilize a wavelength window around 1300 nm, where multimode fibers offer reliable performance for data transmission.
- 1000BASE-SX (770-860 nm) for Gigabit Ethernet (GbE): Optimized for high-speed Ethernet over multimode fiber, this application takes advantage of the lower window around 850 nm.
- 1000BASE-LX (1270-1355 nm) for GbE: This standard extends the use of multimode fibers into the 1300 nm window for Gigabit Ethernet applications.
HIPPI (High-Performance Parallel Interface): This high-speed computer bus architecture utilizes both the 850 nm and the 1300 nm windows, spanning from 830-860 nm and 1260-1360 nm, respectively, to support fast data transfers over multimode fibers.
Future Classifications and Studies
The classification of multimode fibers is a subject of ongoing research. Proposals suggest the use of the region from 770 nm to 910 nm, which could open up new avenues for multimode fiber applications. As technology progresses, these classifications will continue to evolve, reflecting the dynamic nature of fiber optic communications.
Wrapping Up: The Place of Multimode Fibers in Networking
Multimode fibers are a vital part of the networking world, particularly in scenarios that require high data rates over shorter distances. Their resilience to bending and capacity for high bandwidth make them an attractive choice for a variety of applications, from high-speed data transfer in industrial settings to backbone cabling in data centers.
As we continue to study and refine the classifications of multimode fibers, their role in the future of networking is guaranteed to expand, bringing new possibilities to the realm of optical communications.
References
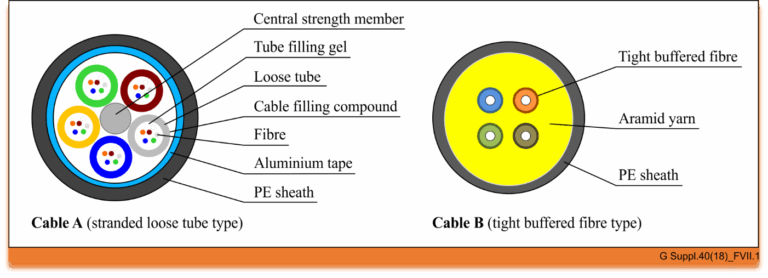
The world of optical communication is intricate, with different cable types designed for specific environments and applications. Today, we’re diving into the structure of two common types of optical fiber cables, as depicted in Figure below, and summarising the findings from an appendix that examined their performance.
Figure
Cable A: The Stranded Loose Tube Outdoor Cable
Cable A represents a quintessential outdoor cable, built to withstand the elements and the rigors of outdoor installation. The cross-section of this cable reveals a complex structure designed for durability and performance:
- Central Strength Member: At its core, the cable has a central strength member that provides mechanical stability and ensures the cable can endure the tensions of installation.
- Tube Filling Gel: Surrounding the central strength member are buffer tubes secured with a tube filling gel, which protects the fibers from moisture and physical stress.
- Loose Tubes: These tubes hold the optical fibers loosely, allowing for expansion and contraction due to temperature changes without stressing the fibers themselves.
- Fibers: Each tube houses six fibers, comprising various types specified by the ITU-T, including G.652.D, G.654.E, G.655.D, G.657.A1, G.657.A2, and G.657.B3. This array of fibers ensures compatibility with different transmission standards and conditions.
- Aluminium Tape and PE Sheath: The aluminum tape provides a barrier against electromagnetic interference, while the polyethylene (PE) sheath offers physical protection and resistance to environmental factors.
The stranded loose tube design is particularly suited for long-distance outdoor applications, providing a robust solution for optical networks that span vast geographical areas.
Cable B: The Tight Buffered Indoor Cable
Switching our focus to indoor applications, Cable B is engineered for the unique demands of indoor environments:
- Tight Buffered Fibers: Unlike Cable A, this indoor cable features four tight buffered fibers, which are more protected from physical damage and easier to handle during installation.
- Aramid Yarn: Known for its strength and resistance to heat, aramid yarn is used to reinforce the cable, providing additional protection and tensile strength.
- PE Sheath: Similar to Cable A, a PE sheath encloses the structure, offering a layer of defense against indoor environmental factors.
Cable B contains two ITU-T G.652.D fibers and two ITU-T G.657.B3 fibers, allowing for a blend of standard single-mode performance with the high bend-resistance characteristic of G.657.B3 fibers, making it ideal for complex indoor routing.
Conclusion
The intricate designs of optical fiber cables are tailored to their application environments. Cable A is optimized for outdoor use with a structure that guards against environmental challenges and mechanical stresses, while Cable B is designed for indoor use, where flexibility and ease of handling are paramount. By understanding the components and capabilities of these cables, network designers and installers can make informed decisions to ensure reliable and efficient optical communication systems.
Reference
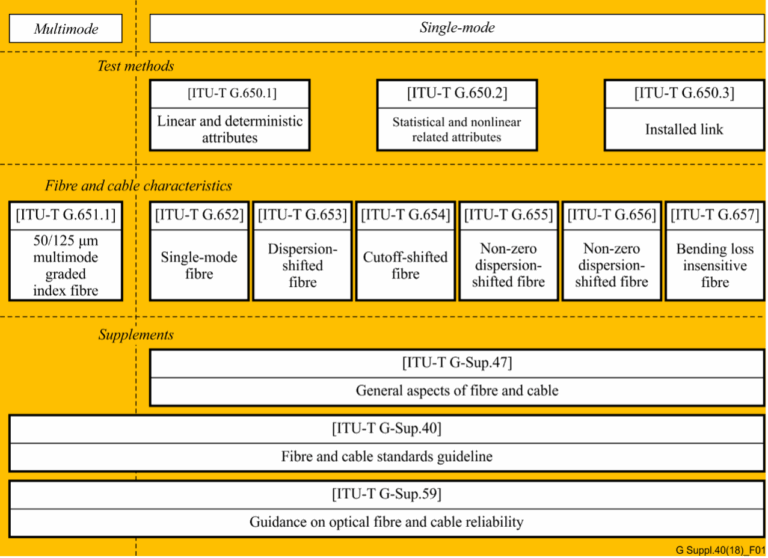
In the realm of telecommunications, the precision and reliability of optical fibers and cables are paramount. The International Telecommunication Union (ITU) plays a crucial role in this by providing a series of recommendations that serve as global standards. The ITU-T G.650.x and G.65x series of recommendations are especially significant for professionals in the field. In this article, we delve into these recommendations and their interrelationships, as illustrated in Figure 1 .
ITU-T G.650.x Series: Definitions and Test Methods
The ITU-T G.650.x series is foundational for understanding single-mode fibers and cables. ITU-T G.650.1 is the cornerstone, offering definitions and test methods for linear and deterministic parameters of single-mode fibers. This includes key measurements like attenuation and chromatic dispersion, which are critical for ensuring fiber performance over long distances.
Moving forward, ITU-T G.650.2 expands on the initial parameters by providing definitions and test methods for statistical and non-linear parameters. These are essential for predicting fiber behavior under varying signal powers and during different transmission phenomena.
For those involved in assessing installed fiber links, ITU-T G.650.3 offers valuable test methods. It’s tailored to the needs of field technicians and engineers who analyze the performance of installed single-mode fiber cable links, ensuring that they meet the necessary standards for data transmission.
ITU-T G.65x Series: Specifications for Fibers and Cables
The ITU-T G.65x series recommendations provide specifications for different types of optical fibers and cables. ITU-T G.651.1 targets the optical access network with specifications for 50/125 µm multimode fiber and cable, which are widely used in local area networks and data centers due to their ability to support high data rates over short distances.
The series then progresses through various single-mode fiber specifications:
- ITU-T G.652: The standard single-mode fiber, suitable for a wide range of applications.
- ITU-T G.653: Dispersion-shifted fibers optimized for minimizing chromatic dispersion.
- ITU-T G.654: Features a cut-off shifted fiber, often used for submarine cable systems.
- ITU-T G.655: Non-zero dispersion-shifted fibers, which are ideal for long-haul transmissions.
- ITU-T G.656: Fibers designed for a broader range of wavelengths, expanding the capabilities of dense wavelength division multiplexing systems.
- ITU-T G.657: Bending loss insensitive fibers, offering robust performance in tight bends and corners.
Historical Context and Current References
It’s noteworthy to mention that the multimode fiber test methods were initially described in ITU-T G.651. However, this recommendation was deleted in 2008, and now the test methods for multimode fibers are referenced in existing IEC documents. Professionals seeking current standards for multimode fiber testing should refer to these IEC documents for the latest guidelines.
Conclusion
The ITU-T recommendations play a critical role in the standardization and performance optimization of optical fibers and cables. By adhering to these standards, industry professionals can ensure compatibility, efficiency, and reliability in fiber optic networks. Whether you are a network designer, a field technician, or an optical fiber manufacturer, understanding these recommendations is crucial for maintaining the high standards expected in today’s telecommunication landscape.