nyquist
Test points, insertion loss allocation, eye limits, link training and client mapping across the short electrical channel …
-
Free
-
August 13, 2026
How the relationship between spectral slot allocation and symbol rate drives... …
-
Premium
-
April 22, 2026
in Optical Fiber Engineering Strategies for Maximizing Spectral Efficiency at the Shannon Limit Introduction: The Quest for Spectral Efficiency The...
-
Free
-
November 19, 2025
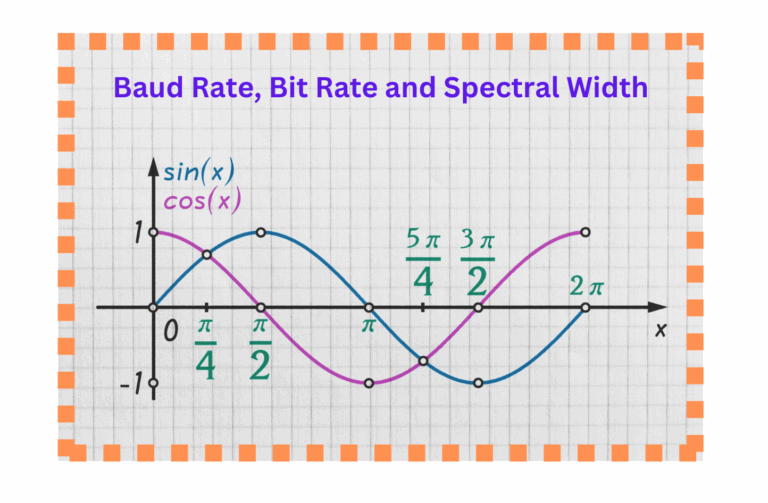
In modern optical fiber communications, maximizing data transmission efficiency while minimizing signal degradation is crucial. Several key parameters such as...
-
Free
-
March 26, 2025
Explore Articles
- Analysis
- Automation
- Careers and Learning Paths
- Coherent Optics
- Data Center Interconnect
- Free
- Fundamentals
- Management
- Network Architecture
- Planning & Design
- Premium
- Professional Development
- Security
- Standards
- Submarine and Long-Haul
- Technical
- Testing
- Tools and Simulators
- Trends & News
- Troubleshooting and Operations
- Vendor and Product Landscape
Filter Articles
ResetTags
400ZR
800ZR
amplifier
automation
behavioral
C+L Band
career
COHERENT
coherent optics
data center interconnect
Dispersion
DWDM
edfa
EDFA noise figure
fec
Fiber optic technology
GSNR
hiring
Interview
Latency
launch power
Link Budget
NETCONF
network automation
noise figure
OFEC
optical
Optical communication
Optical fiber
Optical network
Optical signal-to-noise ratio
OSNR
OTN
Probabilistic Constellation Shaping
raman
repeater
ROADM
Slider
span loss
spectral efficiency
submarine
Submarine Cable
telemetry
Transponder
WSS