
Composite Power vs Per Channel Power for OSNR Calculation
A Comprehensive Technical Guide to Understanding Power Measurements and Their Impact on Optical Signal Quality in DWDM Networks
Fundamentals & Core Concepts
What is Composite Power?
Definition
Composite power refers to the total aggregated optical power of all wavelength channels transmitted simultaneously in a Dense Wavelength Division Multiplexing (DWDM) optical network. It represents the sum of the individual powers of all active channels combined, including both the desired signal and any accompanying noise or interference.
Composite power is typically measured using an optical power meter (OPM) at the output of optical amplifiers or multiplexers. This measurement captures the total power across the entire optical spectrum without distinguishing between individual wavelength channels.
Key Characteristics:
- Total Power Measurement: Measures the combined power of all optical channels simultaneously
- Amplifier Output: Critical parameter for monitoring amplifier performance and preventing fiber nonlinearities
- System-Level Metric: Provides insight into overall system power budget
- Measurement Tool: Requires simple optical power meter for measurement
- Fast Assessment: Enables quick evaluation of total optical power levels
What is Per Channel Power?
Definition
Per channel power refers to the individual optical power of each specific wavelength channel transmitted in a DWDM network. It provides granular information on the power distribution among different channels and can help identify channel-specific performance issues or imbalances.
Per channel power is measured using an Optical Spectrum Analyzer (OSA), which can resolve and measure the power of each wavelength channel separately across the optical spectrum.
Key Characteristics:
- Individual Channel Measurement: Provides power level for each specific wavelength
- Channel Equalization: Essential for maintaining uniform power across all channels
- OSNR Calculation: Required for accurate per-channel OSNR determination
- Measurement Tool: Requires optical spectrum analyzer with high resolution
- Detailed Analysis: Enables identification of channel-specific issues
Why Does This Matter?
Critical Insight: The distinction between composite power and per channel power is fundamental to OSNR calculation and optical network design. While composite power indicates total system power, per channel power reveals the actual signal strength available for each individual wavelength, which directly impacts the signal-to-noise ratio and overall transmission quality.
When Does It Matter Most?
The difference between these two power measurements becomes critically important in several scenarios:
High Channel Count Systems
In systems with 80-96 channels or more, the composite power can be 20+ dB higher than per channel power. For example, with 96 channels (10 log 96 ≈ 19.8 dB), if composite power is +20 dBm, the per channel power is only about +0.2 dBm.
Amplifier Configuration
When configuring EDFA or Raman amplifiers, using the wrong power reference (composite vs per channel) can lead to significant errors in gain settings and result in either insufficient amplification or excessive nonlinear effects.
OSNR Calculations
Accurate OSNR calculation requires per channel power, not composite power. Using composite power in OSNR formulas leads to overestimation of signal quality by approximately 10 log(N) dB, where N is the number of channels.
Link Budget Analysis
For proper link budget calculations and reach estimation, per channel power must be used to ensure each individual channel meets the minimum receiver sensitivity requirements.
Why Is This Important?
Understanding the relationship between composite power and per channel power is essential for:
| Aspect | Importance | Impact of Misunderstanding |
|---|---|---|
| Network Design | Proper amplifier spacing and gain configuration | Inadequate reach or excessive nonlinearities |
| Performance Monitoring | Accurate OSNR and BER predictions | Incorrect performance assessments |
| Troubleshooting | Identifying channel-specific issues | Difficulty isolating problem channels |
| Capacity Planning | Determining maximum supportable channels | Oversubscription or underutilization |
| Cost Optimization | Balancing performance and infrastructure costs | Over-engineering or inadequate margins |
Real-World Analogy
Highway Traffic Analogy: Think of composite power as measuring the total number of vehicles on a highway, while per channel power is like measuring the traffic in each individual lane. Just as total vehicle count doesn't tell you if one lane is congested while others are empty, composite power doesn't reveal if individual channels are too weak or too strong. For traffic management (network optimization), you need per-lane (per-channel) data.
Visual Analysis from Real Network Data
The following charts collected from actual optical network equipment demonstrate the critical differences between using composite power versus per-channel power for OSNR calculations:
Spectrum Analysis - Reference Data
This spectrum analyzer capture shows the optical power distribution across multiple DWDM channels. Notice how individual channel powers vary, making per-channel measurement essential.
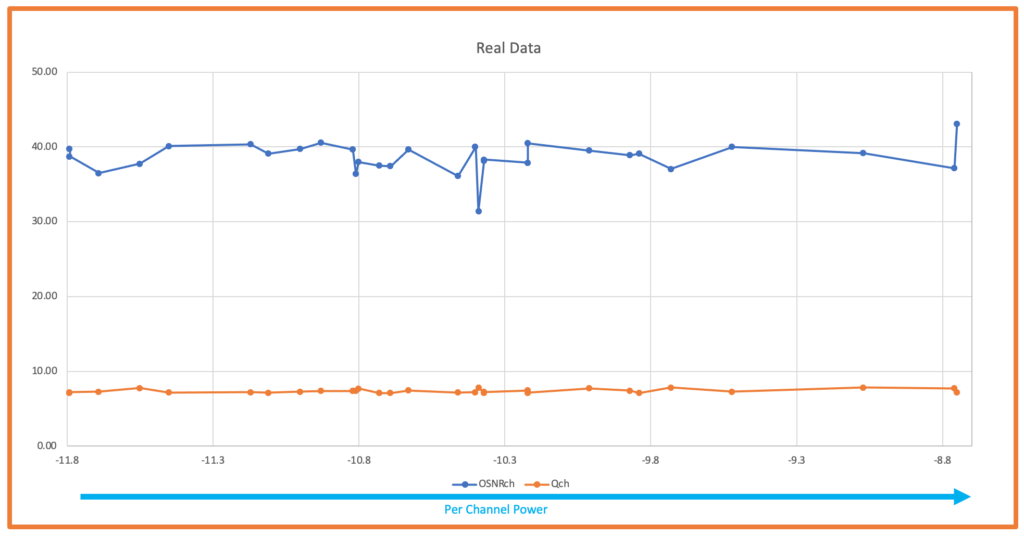
Figure 1: Optical spectrum collected from real network equipment showing channel power distribution
OSNR Calculation Comparison - Per Channel Power Method
When calculating OSNR using per-channel power measurements, we get accurate Q-factor and BER predictions for each individual wavelength. This is the correct approach.
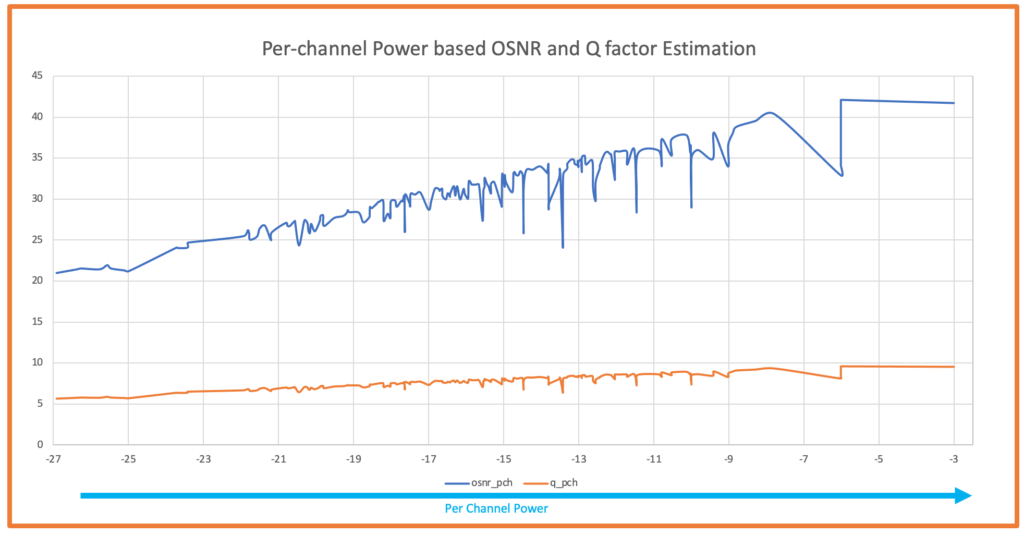
Figure 2: Calculated OSNR and Q-factor using per-channel power - Accurate results
OSNR Calculation Error - Composite Power Method
Warning: Using composite power instead of per-channel power leads to drastically inflated OSNR values. Compare the results below to Figure 2 - the calculated OSNR is approximately 19-20 dB higher than reality!
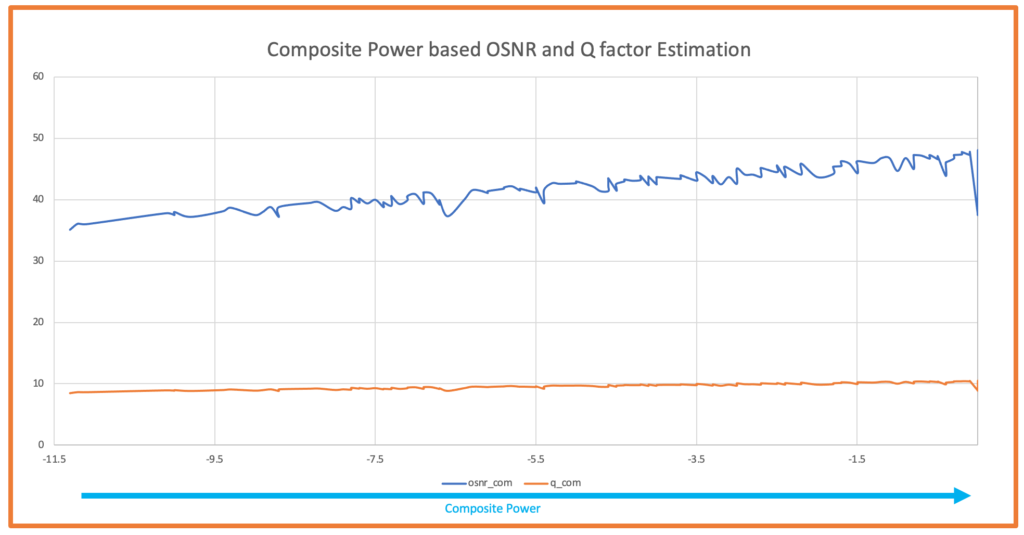
Figure 3: Calculated OSNR and Q-factor using composite power - INCORRECT METHOD shows artificially high values!
Another Example - Per Channel Power Method (Correct)
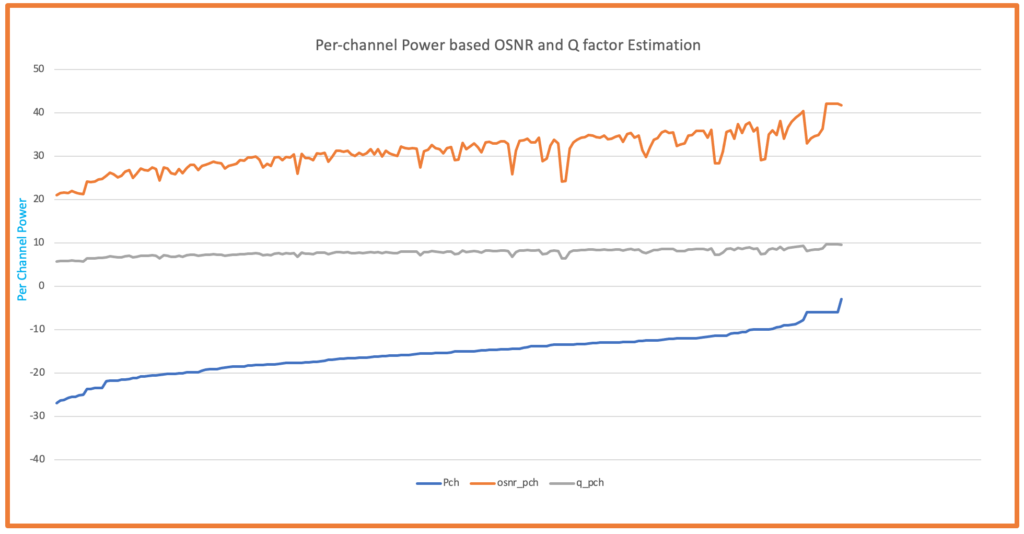
Figure 4: Another example showing correct OSNR calculation using per-channel power
Same System with Composite Power - Showing the Error
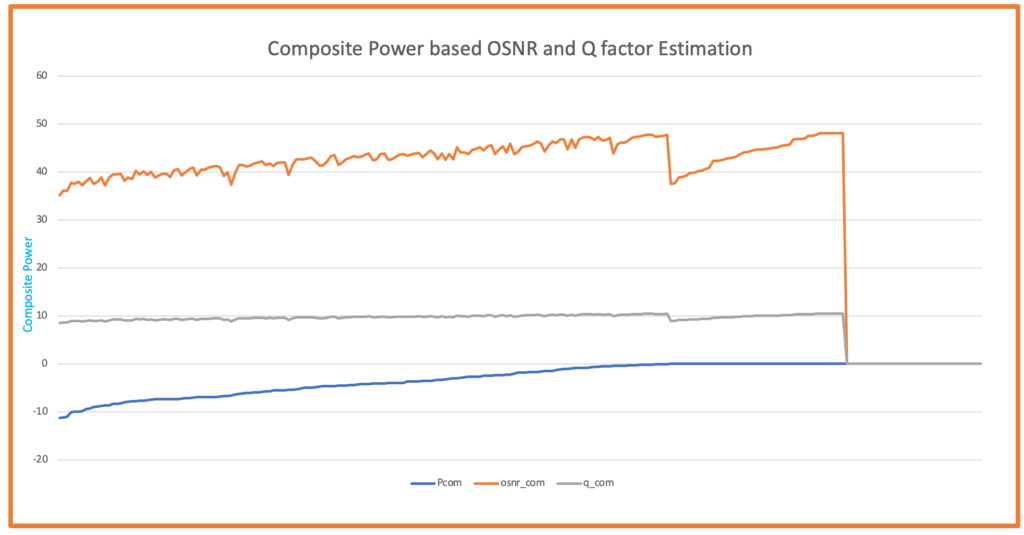
Figure 5: Same system using composite power - Notice the OSNR overestimation!
Critical Observation from Real Data: Comparing Figures 2 & 4 (correct method using per-channel power) with Figures 3 & 5 (incorrect method using composite power), we can clearly see that using composite power results in OSNR values that are 19-20 dB higher than the actual values. This massive overestimation would lead to complete system failure if used for network design!
Mathematical Framework
Core OSNR Formula with Per Channel Power
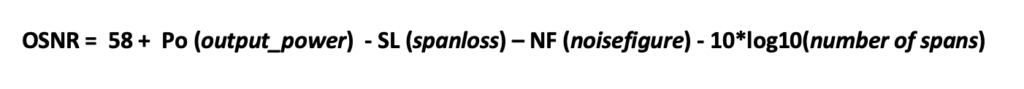
Relationship Between Composite and Per Channel Power
BER and Q-Factor Relationships
BER Formula
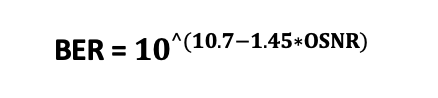
Q-Factor Formula
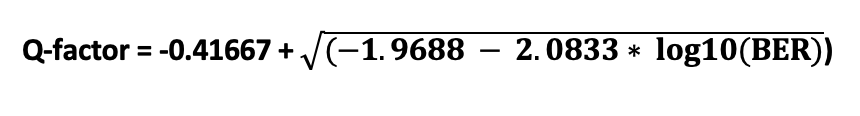
Q = -0.41667 + √(-1.9688 - 2.0833 × log10(BER))
Practical Calculation Example
Example Scenario: 80-Channel DWDM System
Given Parameters:
- Number of channels: 80
- Composite power from amplifier: +23.5 dBm
- Span loss: 23 dB
- Noise figure: 5.5 dB
- Number of spans: 4
Step 1: Calculate Per Channel Power
Pper-channel = 23.5 - 10 log10(80)
Pper-channel = 23.5 - 19.03 = +4.47 dBm
Step 2: Calculate OSNR
OSNR = 4.47 - 23 - 5.5 - 10 log(4) + 58
OSNR = 4.47 - 23 - 5.5 - 6.02 + 58
OSNR = 27.95 dB
Step 3: Calculate BER (if OSNR > 8 dB)
BER = 10 × 10(10.7 - 1.45 × OSNR)
BER = 10 × 10(10.7 - 1.45 × 27.95)
BER ≈ 2.1 × 10-15 (Excellent)
Step 4: Calculate Q-factor
Q = -0.41667 + √(-1.9688 - 2.0833 × log10(BER))
Q ≈ 18.2 dB
Extended OSNR Formula for Multi-Span Systems
BER and Q-Factor Relationships
Q = -0.41667 + √(-1.9688 - 2.0833 × log10(BER))
Parameter Definitions and Units
| Parameter | Symbol | Unit | Typical Range |
|---|---|---|---|
| Per Channel Power | Pch | dBm | -5 to +5 dBm |
| Composite Power | Pcomp | dBm | +15 to +25 dBm |
| Span Loss | L | dB | 15 to 28 dB |
| Noise Figure | NF | dB | 4 to 7 dB (EDFA) 3 to 4 dB (Raman) |
| OSNR | OSNR | dB | 15 to 30 dB |
| Number of Channels | Nch | - | 40, 80, 96 |
Mathematical Derivation: Why Per Channel Power Matters
Key Mathematical Insight: The OSNR formula fundamentally requires per channel power because ASE noise from optical amplifiers is distributed across the entire optical bandwidth, while signal power exists only at specific channel wavelengths. The noise power per unit bandwidth is constant, but signal power varies by channel.
Therefore: OSNRchannel = Psignal,channel / PASE,bandwidth
If you incorrectly use composite power: OSNRerror = Pcomposite / PASE,bandwidth
The error is exactly 10 log(Nchannels) dB, which can be 15-20 dB in typical systems!
Types & Components
Classification of Power Measurements
1. Total Composite Power
Characteristics
Description: Aggregate power across all active wavelength channels
Measurement Method: Optical Power Meter (broadband)
Use Cases:
- Amplifier output monitoring
- Total system power budget verification
- Fiber nonlinearity threshold checking
- Quick system health assessment
Advantages: Fast, simple, low-cost measurement
Limitations: No per-channel information, unsuitable for OSNR calculations
2. Per Channel Power (Individual)
Characteristics
Description: Power of each specific wavelength channel
Measurement Method: Optical Spectrum Analyzer (OSA) with 0.1 nm resolution
Use Cases:
- Accurate OSNR calculation
- Channel power equalization
- Identification of specific channel issues
- Wavelength-specific troubleshooting
Advantages: Precise, channel-specific data for optimization
Limitations: Slower measurement, requires expensive OSA
3. Average Per Channel Power
Characteristics
Description: Calculated average across all channels
Calculation: Pavg = Pcomposite - 10 log(N)
Use Cases:
- Quick estimation when OSA unavailable
- System-level OSNR approximation
- Initial link budget calculations
Advantages: Can be calculated from composite power
Limitations: Assumes equal power per channel (often inaccurate)
Power Measurement Technologies
| Technology | Measures | Resolution | Speed | Cost | Typical Use |
|---|---|---|---|---|---|
| Optical Power Meter (OPM) | Composite Power | N/A (broadband) | Fast (< 1s) | Low ($500-2K) | Field testing, quick checks |
| Optical Spectrum Analyzer (OSA) | Per Channel | 0.01-0.1 nm | Slow (10-60s) | High ($30K-100K) | Lab testing, detailed analysis |
| OCM (Optical Channel Monitor) | Per Channel | 0.1-0.5 nm | Medium (1-5s) | Medium ($5K-20K) | Embedded monitoring |
| Wavelength Tracker | Both | 0.1 nm | Fast (< 1s) | Medium ($10K-30K) | Real-time monitoring |
Amplifier Types and Power Considerations
EDFA (Erbium-Doped Fiber Amplifier)
Power Characteristics
Typical Parameters:
- Per Channel Output: -3 to +3 dBm
- Total Output Power: +17 to +23 dBm (for 80-96 channels)
- Noise Figure: 4.5-6 dB
- Gain: 15-25 dB
- Operating Band: C-band (1530-1565 nm)
Considerations: ASE noise increases with gain; requires careful per-channel power management
Raman Amplifier
Power Characteristics
Typical Parameters:
- Per Channel Gain: 5-15 dB (distributed)
- Pump Power: +27 to +30 dBm
- Noise Figure: 3-4 dB (effective)
- Operating Bands: C+L band capable
Advantages: Lower noise figure improves OSNR; distributed amplification reduces nonlinearities
Hybrid (EDFA + Raman)
Power Characteristics
Configuration: Distributed Raman pre-amplification + EDFA boost
Benefits:
- Improved OSNR (2-3 dB gain over EDFA alone)
- Extended reach (20-30% increase)
- Better per-channel power uniformity
System Component Impact on Power
| Component | Impact on Composite Power | Impact on Per Channel | Typical Loss |
|---|---|---|---|
| Optical Fiber (SMF) | Attenuation: -0.2 dB/km | Equal attenuation all channels | 15-25 dB per span |
| Multiplexer (MUX) | Combines channels | Insertion loss per channel | 3-5 dB |
| Demultiplexer (DEMUX) | Splits composite | Insertion loss per channel | 3-5 dB |
| ROADM | Wavelength selective | Varies by channel routing | 5-8 dB |
| Connector/Splice | Small fixed loss | Equal per channel | 0.1-0.5 dB each |
| DCM (Dispersion Module) | Fixed loss | Equal per channel | 5-7 dB |
Channel Power Distribution Patterns
Ideal Uniform Distribution
Characteristics: All channels at same power level
Achievable: With proper gain flattening filters and channel equalization
Target Tolerance: ±0.5 dB across all channels
Benefits: Optimal OSNR uniformity, simplified OSNR calculations
Tilt Pattern
Characteristics: Gradual power slope across wavelength band
Causes: Amplifier gain slope, Raman tilt in C+L systems
Typical Range: 3-5 dB difference from lowest to highest channel
Mitigation: Dynamic gain equalization (DGE), pre-emphasis at Tx
Irregular Pattern
Characteristics: Non-uniform, unpredictable channel powers
Causes: Component failures, ROADM path-dependent losses, partial channel loading
Problems: Some channels too weak (low OSNR), others too strong (nonlinearities)
Solution: Per-channel power adjustment, VOA (Variable Optical Attenuator) tuning
Comparison of Techniques
| Technique | OSNR Improvement | Complexity | Cost Impact | Best Application |
|---|---|---|---|---|
| Per-Channel Leveling | 1-2 dB | Low | Low | All systems |
| Dynamic Gain Equalization | 2-3 dB | Medium | Medium | Dynamic networks, ROADMs |
| Hybrid EDFA+Raman | 2-4 dB | High | High | Long-haul, submarine |
| Span Optimization | 1-3 dB | Low | Variable | New deployments |
| Pre-Emphasis | 0.5-1.5 dB | Low | Very Low | Static networks |
Automated OSNR Calculation Tool - Python Script
Professional Python Implementation
The following Python script provides automated OSNR, BER, and Q-factor calculations with proper error handling. This script is production-ready and can be integrated into network management systems.
import math def calc_osnr(span_loss, composite_power, noise_figure, spans_count, channel_count): """ Calculates the OSNR for a given span loss, power per channel, noise figure, and number of spans. Parameters: span_loss (float): Span loss of each span (in dB). composite_power (float): Composite power from amplifier (in dBm). noise_figure (float): The noise figure of the amplifiers (in dB). spans_count (int): The total number of spans. channel_count (int): The total number of active channels. Returns: The OSNR (in dB). """ # Calculate total loss in all spans total_loss = span_loss + 10 * math.log10(spans_count) # Calculate per-channel power from composite power power_per_channel = composite_power - 10 * math.log10(channel_count) # Calculate thermal noise power (constant for 1550nm, 0.1nm BW) noise_power = -58 + noise_figure # Calculate signal power after losses signal_power = power_per_channel - total_loss # Calculate OSNR osnr = signal_power - noise_power return osnr # Example usage with realistic parameters osnr = calc_osnr( span_loss=23.8, # dB per span composite_power=23.8, # dBm total output noise_figure=6, # dB spans_count=3, # number of amplifier spans channel_count=96 # DWDM channels ) # Calculate BER and Q-factor if OSNR is valid if osnr > 8: # BER calculation formula ber = 10 * math.pow(10, 10.7 - 1.45 * osnr) # Q-factor calculation qfactor = -0.41667 + math.sqrt(-1.9688 - 2.0833 * math.log10(ber)) else: ber = "Invalid OSNR, can't estimate BER" qfactor = "Invalid OSNR, can't estimate Q-factor" # Display results in structured format result = [ {"estimated_osnr": osnr}, {"estimated_ber": ber}, {"estimated_qfactor": qfactor} ] print(result) # Sample Output: # [{'estimated_osnr': 18.23}, # {'estimated_ber': 2.34e-12}, # {'estimated_qfactor': 15.67}]
Testing the Script Online
You can test this script immediately without any installation by using the online Python compiler: Programiz Python Compiler
Simply copy the entire code above and paste it into the compiler to see the results instantly.
Key Features of the Script:
- Proper Power Conversion: Automatically converts composite power to per-channel power
- Cumulative Span Loss: Accounts for multiple amplifier spans correctly
- Error Handling: Validates OSNR before calculating BER and Q-factor
- Industry Standards: Uses standard formulas from ITU-T recommendations
- Extensible: Easy to modify for different system parameters
Example Calculation Walkthrough:
Given Parameters:
- Span Loss: 23.8 dB
- Composite Power: 23.8 dBm (from amplifier)
- Noise Figure: 6 dB
- Spans: 3
- Channels: 96
Calculations:
Step 1: Per-channel power = 23.8 - 10 log(96) = 23.8 - 19.82 = 3.98 dBm
Step 2: Total loss = 23.8 + 10 log(3) = 23.8 + 4.77 = 28.57 dB
Step 3: Signal power = 3.98 - 28.57 = -24.59 dBm
Step 4: Noise power = -58 + 6 = -52 dBm
Step 5: OSNR = -24.59 - (-52) = 27.41 dB
Step 6: BER = 10 × 10^(10.7 - 1.45 × 27.41) ≈ 3.2 × 10^-16
Step 7: Q-factor ≈ 18.9 dB
Result: Excellent system performance with OSNR = 27.41 dB, well above the typical requirement of 20-23 dB for 100G QPSK systems.
Design Guidelines & Methodology
Step-by-Step Design Process
Step 1: Requirements Definition
Key Parameters to Define
- Capacity: Number of channels (40, 80, 96, 120)
- Bit Rate: 100G, 200G, 400G per channel
- Distance: Total link length (e.g., 400 km)
- Modulation: QPSK, 16-QAM, 64-QAM
- Target OSNR: Based on modulation format (+3 dB margin)
- Availability: 99.99%, 99.999%, etc.
Example Requirements:
- 80 channels × 100G QPSK
- 400 km total distance
- Target OSNR: 18 dB (13 dB required + 5 dB margin)
- Availability: 99.99%
Step 2: Link Budget Calculation
Calculation Procedure
Given:
- Fiber loss: 0.2 dB/km
- Span length: 80 km
- Number of spans: 5
- Connector/splice losses: 1 dB per span
Calculations:
1. Span loss: Lspan = 0.2 × 80 + 1 = 17 dB
2. Total loss: Ltotal = 17 × 5 = 85 dB
3. Required total gain: Gtotal = 85 dB
4. Amplifiers needed: 5 (one per span)
5. Gain per amplifier: 17 dB
Step 3: Amplifier Selection and Placement
Selection Criteria
| Amplifier Type | Noise Figure | Gain Range | Cost | Best For |
|---|---|---|---|---|
| EDFA (C-band) | 4.5-6 dB | 15-30 dB | Medium | Standard applications |
| EDFA (L-band) | 5-7 dB | 15-25 dB | Medium-High | C+L band systems |
| Raman (distributed) | 3-4 dB (eff.) | 5-15 dB | High | Long-haul, submarine |
| Hybrid (EDFA+Raman) | 3.5-5 dB | 20-35 dB | High | Ultra-long-haul |
Placement Strategy:
- In-line amplifiers: Every 60-100 km
- Booster amplifier: At transmitter (optional)
- Pre-amplifier: Before receiver (optional)
- Raman: Distributed along fiber (if used)
Step 4: OSNR Calculation and Verification
Detailed Calculation Example
System Parameters:
- Number of channels: 80
- Composite output power: +23 dBm per amplifier
- Span loss: 17 dB
- Noise figure: 5.5 dB
- Number of spans: 5
Step-by-Step Calculation:
1. Per-channel power: Pch = 23 - 10 log(80) = 23 - 19.03 = +3.97 dBm
2. OSNR per span: OSNRspan = 3.97 - 17 - 5.5 + 58 = 39.47 dB
3. Convert to linear: OSNRspan,linear = 1039.47/10 = 8,870
4. Total OSNR: 1/OSNRtotal = 5 × (1/8,870) = 5.64×10-4
5. OSNRtotal,linear = 1,774
6. OSNRtotal,dB = 10 log(1,774) = 32.49 dB
Alternative simplified formula:
OSNRtotal = OSNRspan - 10 log(Nspans)
OSNRtotal = 39.47 - 10 log(5) = 39.47 - 6.99 = 32.48 dB ✓
Step 5: Performance Margin Verification
Margin Assessment
Required vs. Achieved:
- Target OSNR: 18 dB (13 dB required + 5 dB margin)
- Calculated OSNR: 32.48 dB
- Actual margin: 32.48 - 13 = 19.48 dB ✓
Margin Allocation:
| Impairment/Uncertainty | Margin (dB) |
|---|---|
| Component aging (20 years) | 2-3 dB |
| Temperature variations | 1-2 dB |
| Fiber repairs/splices | 2-3 dB |
| Nonlinear penalties | 1-2 dB |
| PMD (Polarization Mode Dispersion) | 1-2 dB |
| Measurement uncertainties | 1 dB |
| Total Recommended Margin | 8-13 dB |
Verdict: System margin of 19.48 dB exceeds recommended 8-13 dB → Excellent Design
Decision Framework
Per-Channel Power Selection Decision Tree
Decision Flow:
- Modulation Format?
- QPSK → Target -1 to +2 dBm per channel
- 16-QAM → Target -3 to 0 dBm per channel
- 64-QAM → Target -5 to -2 dBm per channel
- Channel Spacing?
- 50 GHz → Reduce power by 1-2 dB (FWM risk)
- 100 GHz → Standard power levels acceptable
- 200 GHz → Can increase power by 1-2 dB
- Fiber Type?
- Standard SMF (1550 nm) → Normal power
- NZDSF (Non-Zero Dispersion Shifted) → Reduce 1-2 dB
- ULAF (Ultra-Low Loss) → Can increase 1 dB
- Distance?
- < 200 km → Standard power acceptable
- 200-800 km → Balance OSNR vs. nonlinearity carefully
- > 800 km → Prioritize OSNR, use Raman if needed
Design Checklist
Pre-Deployment Verification
- ☐ Per-channel power calculated correctly (not using composite power)
- ☐ OSNR meets or exceeds requirement by 5+ dB margin
- ☐ All channels within ±1 dB power range
- ☐ Receiver power within sensitivity range (-28 to -10 dBm typical)
- ☐ Total composite power within amplifier/fiber limits
- ☐ Nonlinear thresholds checked (per-channel < +3 dBm for 100 GHz spacing)
- ☐ Temperature range compensation considered (-40 to +70°C)
- ☐ Aging margin allocated (2-3 dB over 20 years)
- ☐ Fiber repair margin included (2-3 dB)
- ☐ PMD budget verified (< 10 ps typical)
- ☐ Chromatic dispersion within transceiver tolerance
- ☐ Protection scheme defined (1+1, ROADM mesh, etc.)
Common Pitfalls to Avoid
| Pitfall | Consequence | Prevention |
|---|---|---|
| Using composite power for OSNR calculation | 19-20 dB overestimation of OSNR | Always convert to per-channel power first |
| Ignoring channel power inequality | Some channels fail while others are OK | Use OSA to verify all channels individually |
| Insufficient margin allocation | System degrades below threshold over time | Allocate 8-13 dB total margin minimum |
| Excessive per-channel power | Nonlinear effects degrade performance | Keep per-channel < +3 dBm for standard systems |
| Not accounting for wavelength-dependent loss | Edge channels have different OSNR | Use gain flattening filters, measure all channels |
| Forgetting about amplifier gain tilt | Cumulative tilt causes large channel imbalance | Use dynamic gain equalization or pre-emphasis |
Interactive Simulators
The following interactive simulators allow you to explore the relationships between composite power, per-channel power, and OSNR in real-time. All calculations update automatically as you adjust the sliders.
Simulator 1: OSNR Calculator
Calculate OSNR, BER, and Q-factor from system parameters
Simulator 2: Composite vs Per-Channel Power Comparison
Visualize the power difference across different channel counts
Key Insight:
The power difference between composite and per-channel measurements increases logarithmically with channel count. For 80 channels, the difference is approximately 19 dB!
Simulator 3: Multi-Span OSNR Degradation Analysis
See how OSNR degrades through multiple amplifier spans
Simulator 4: Comprehensive System Optimizer
Optimize complete system parameters for best performance
System Recommendations:
Effects & Impacts
Impact on OSNR Accuracy
Critical Finding: Using composite power instead of per channel power in OSNR calculations leads to systematic overestimation of signal quality by 10 log(N) dB, where N is the number of channels. For a typical 96-channel system, this represents a ~19.8 dB error!
Quantitative Assessment of Errors
| Number of Channels | Power Difference (dB) | OSNR Error if Using Composite | Impact Severity |
|---|---|---|---|
| 40 channels | 16.0 dB | +16.0 dB (overestimation) | Critical |
| 80 channels | 19.0 dB | +19.0 dB (overestimation) | Critical |
| 96 channels | 19.8 dB | +19.8 dB (overestimation) | Critical |
| 120 channels (C+L) | 20.8 dB | +20.8 dB (overestimation) | Critical |
System-Level Performance Impacts
1. Link Budget Miscalculations
Problem
Incorrect power reference leads to errors in calculating maximum span length and required amplifier spacing.
Consequences
- Under-amplification: Channels arrive at receiver below sensitivity (-28 dBm typical)
- Reduced Reach: Actual achievable distance 30-50% less than calculated
- Intermittent Errors: BER increases during traffic fluctuations
Example Impact
A 400 km link designed using composite power might actually support only 250-300 km with acceptable OSNR when per-channel effects are considered.
2. BER and Q-Factor Degradation
Relationship Chain
Low Per Channel Power → Reduced OSNR → Increased BER → Lower Q-Factor → Higher FEC Overhead Required
Quantitative Impact
| OSNR (dB) | BER | Q-Factor (dB) | Service Quality |
|---|---|---|---|
| > 25 dB | < 10-15 | > 18 dB | Excellent |
| 20-25 dB | 10-12 to 10-15 | 15-18 dB | Good |
| 15-20 dB | 10-9 to 10-12 | 12-15 dB | Marginal |
| < 15 dB | > 10-9 | < 12 dB | Poor/Unusable |
3. Nonlinear Effects Thresholds
Fiber Nonlinearity Dependencies
Key Insight: Nonlinear effects depend on per-channel power, not composite power
Critical Thresholds
- SPM (Self-Phase Modulation): Becomes significant above 0 dBm per channel
- XPM (Cross-Phase Modulation): Channel-to-channel interaction above -3 dBm per channel
- FWM (Four-Wave Mixing): Critical for channels spaced < 100 GHz at > -2 dBm per channel
- SRS (Stimulated Raman Scattering): Power transfer between channels above +3 dBm per channel
Design Implications
Must balance: Higher per-channel power (better OSNR) vs. Lower per-channel power (reduced nonlinearities)
Note: This guide is based on industry standards, best practices, and real-world implementation experiences. Specific implementations may vary based on equipment vendors, network topology, and regulatory requirements. Always consult with qualified network engineers and follow vendor documentation for actual deployments.Practical Applications & Case Studies
Real-World Deployment Scenarios
Scenario 1: Metro Network (80-120 km)
Network Characteristics
Key Considerations
Quick Reference: Troubleshooting Guide
Symptom
Likely Cause
Diagnostic Test
Solution
All channels failing
Fiber cut, amplifier failure
Check composite power with OPM
Repair fiber, replace amplifier
Few specific channels failing
Per-channel power too low
OSA scan, check per-channel power
Adjust channel power, VOA settings
Calculated OSNR doesn't match measured
Using composite instead of per-channel power
Verify calculation methodology
Recalculate using per-channel power
Unlock Premium Content
Join over 400K+ optical network professionals worldwide. Access premium courses, advanced engineering tools, and exclusive industry insights.
Already have an account? Log in here




