EDFAs
In the world of fiber-optic communication, the integrity of the transmitted signal is critical. As an optical engineers, our primary...
-
Free
-
March 26, 2025
When we talk about the internet and data, what often comes to mind are the speeds and how quickly we...
-
Free
-
March 26, 2025
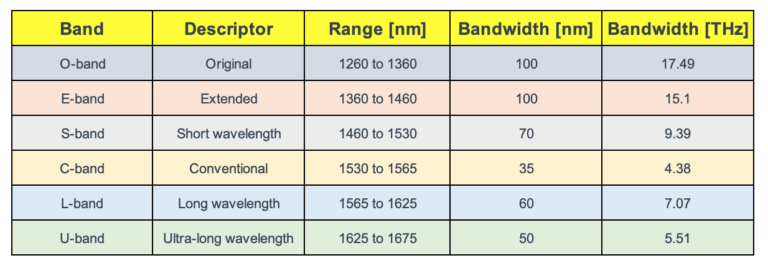
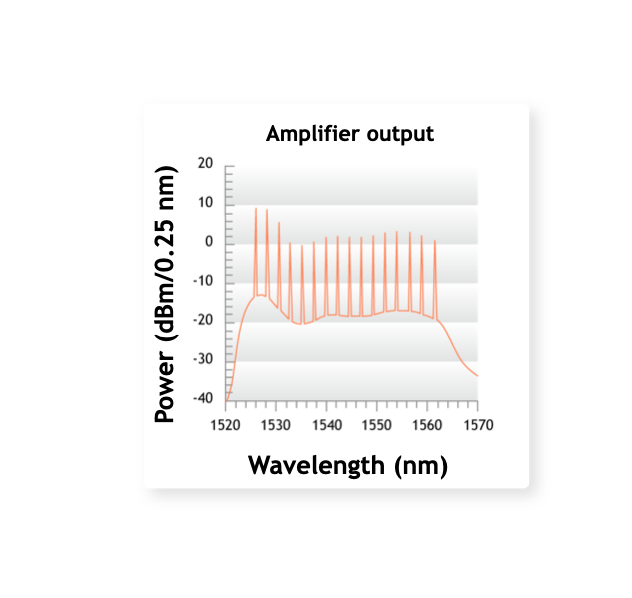
The main advantages and drawbacks of EDFAs are as follows. Advantages Commercially available in C band (1,530 to 1,565 nm)...
-
Free
-
March 26, 2025
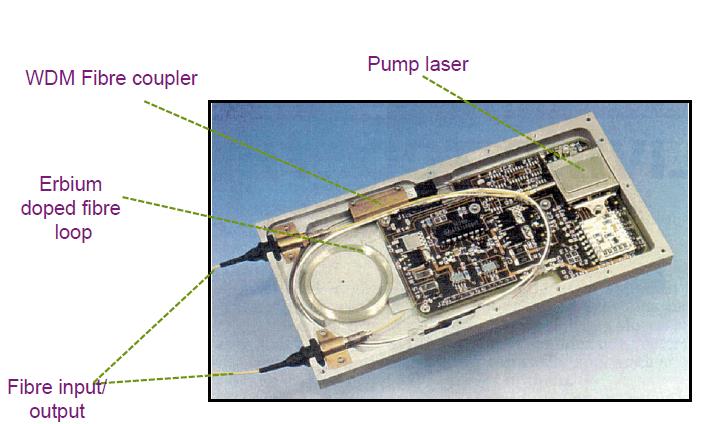
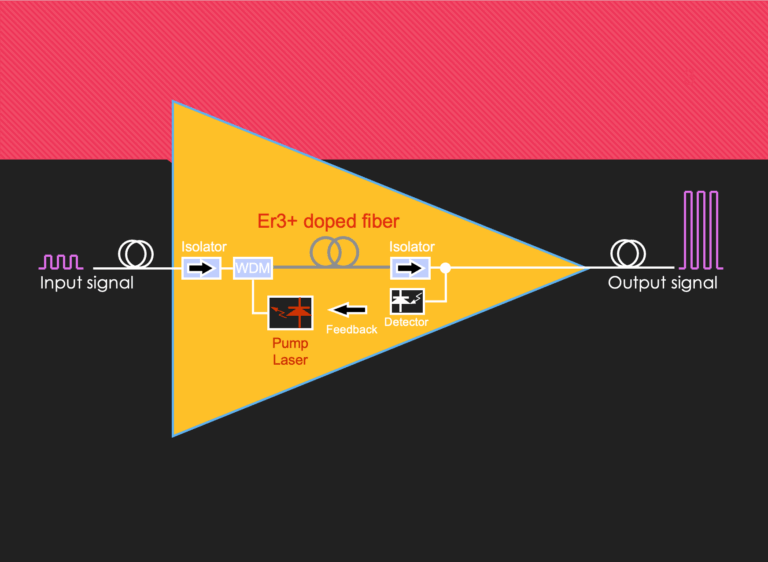
The 980nm pump needs three energy level for radiation while 1480nm pumps can excite the ions directly to the metastable...
-
Free
-
March 26, 2025
A short discussion on 980nm and 1480nm pump based EDFA Introduction The 980nm pump needs three energy level for radiation...
-
Free
-
March 26, 2025
Explore Articles
Filter Articles
ResetTags
amplifier
automation
ber
Bit Error Ratio
Chromatic Dispersion
Communication technology
Data transmission
DWDM
edfa
EDFAs
Erbium-Doped Fiber Amplifiers
Error correction
fec
Fiber optics
Fiber optic technology
Forward Error Correction
Latency
modulation
network automation
Network Design
network management
Network performance
noise figure
optical
optical amplifiers
Optical communication
Optical fiber
Optical network
optical networking
Optical networks
Optical signal-to-noise ratio
Optical transmission
OSNR
OTN
Q-factor
raman
Raman Amplifier
SDH
Signal amplification
Signal distortion
Signal integrity
Signal quality
Slider
Telecommunications
Ticker