SDH
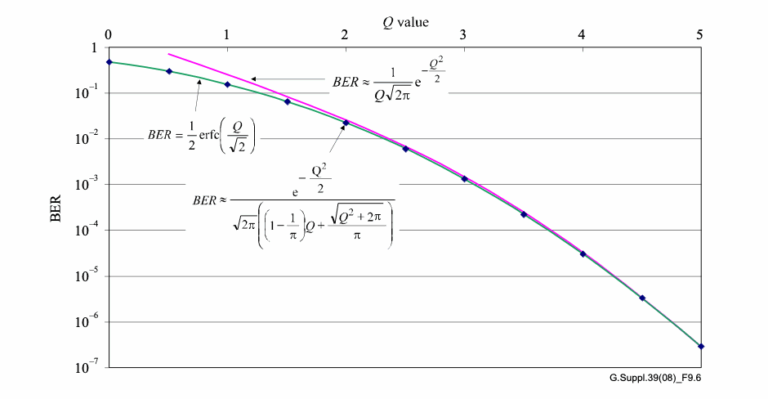
Signal integrity is the cornerstone of effective fiber optic communication. In this sphere, two metrics stand paramount: Bit Error Ratio...
-
Free
-
March 26, 2025
If SDH is based on node and signal synchronization, why do fluctuations occur?Very general question for a Optics beginner. The...
-
Free
-
March 26, 2025
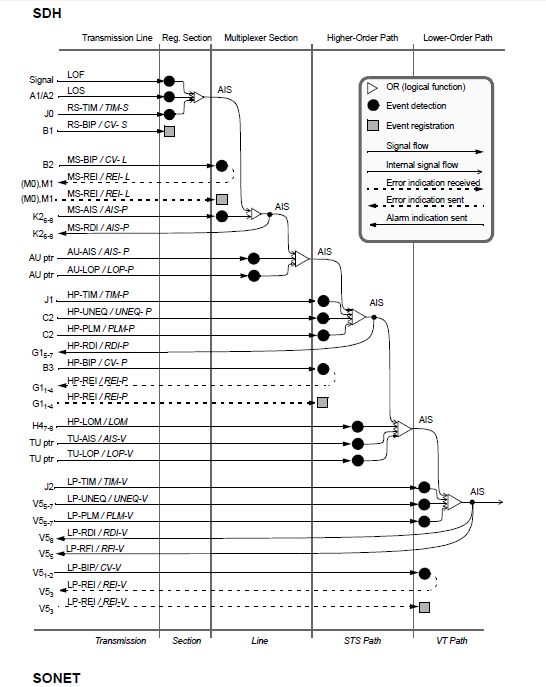
SDH/SONET:Maintenance and Performance Events We know SDH/SONET is older technology now but just have a glimpse for the revision of...
-
Free
-
March 26, 2025
Actually SPE(synchronous payload envelope) can start anywhere within the SONET payload, which necessitates the need for a pointer to point to...
-
Free
-
March 26, 2025
Explore Articles
- Analysis
- Automation
- Careers and Learning Paths
- Coherent Optics
- Data Center Interconnect
- Free
- Fundamentals
- Management
- Network Architecture
- Planning & Design
- Premium
- Security
- Standards
- Submarine and Long-Haul
- Technical
- Testing
- Tools and Simulators
- Trends & News
- Troubleshooting and Operations
- Vendor and Product Landscape
Filter Articles
ResetTags
automation
ber
Chromatic Dispersion
Coherent detection
coherent optical transmission
coherent optics
Data transmission
distributed Raman amplification
DWDM
edfa
EDFA noise figure
fec
Fiber optics
Fiber optic technology
Forward Error Correction
Latency
modulation
network automation
noise figure
optical
Optical communication
Optical fiber
Optical network
optical network automation
Optical network design
optical networking
Optical networks
Optical signal-to-noise ratio
OSNR
OSNR calculation
OTN
Probabilistic Constellation Shaping
Q-factor
raman
Raman amplification
Raman Amplifier
ROADM
Signal integrity
Signal quality
Slider
spectral efficiency
submarine
submarine cable systems
Telecommunications
Ticker