The Bit Error Ratio (BER) is often specified as a performance parameter of a transmission system, which needs to be verified during investigation. Designing an experiment to demonstrate adequate BER performance is not, however, as straightforward as it appears since the number of errors detected over a practical measurement time is generally small. It is, therefore, not sufficient to quote the BER as simply the ratio of the number of errors divided by the number of bits transmitted during the measurement period, instead some knowledge of the statistical nature of the error distribution must first be assumed.
The bit error rate (BER) is the most significant performance parameter of any digital communications system. It is a measure of the probability that any given bit will have been received in error. For example a standard maximum bit error rate specified for many systems is 10-9. This means that the receiver is allowed to generate a maximum of 1 error in every 109 bits of information transmitted or, putting it another way, the probability that any received bit is in error is 10-9.
The BER depends primarily on the signal to noise ratio (SNR) of the received signal which in turn is determined by the transmitted signal power, the attenuation of the link, the link dispersion and the receiver noise. The S/N ratio is generally quoted for analog links while the bit-error-rate (BER) is used for digital links. BER is practically an inverse function of S/N. There must be a minimum power at the receiver to provide an acceptable S/N or BER. As the power increases, the BER or S/N improves until the signal becomes so high it overloads the receiver and receiver performance degrades rapidly.
The formula used to calculate residual BER assumes a gaussian error distribution:
C = 1 – e–nb
C = Degree of confidence required
(0.95 = 95% confidence)
n = No. of bits examined with no error found.
b = Upper bound on BER with a confidence C
(b = 10–15)
To determine the length of time, that is, the number of bits needed to test for (at a given bit rate), requires the above equation to be transposed:
n = loge(1 – C)/b
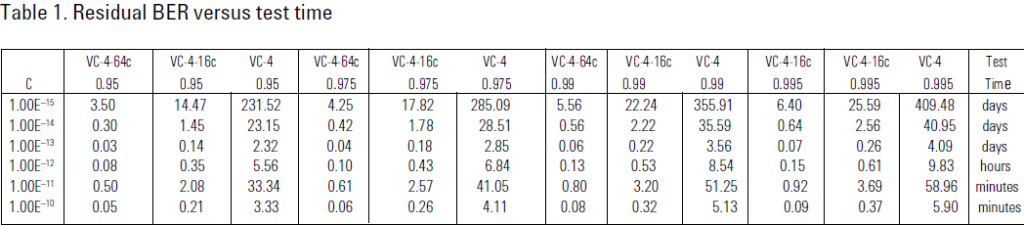
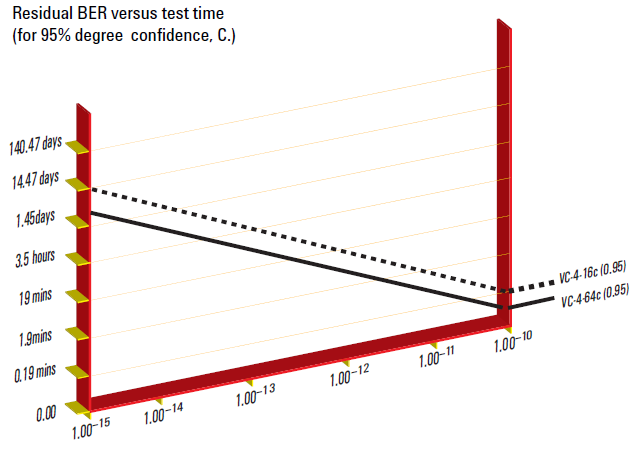
So, to test for a residual BER of 10–13 with a 95% confidence limit requires a test pattern equal to 3 x 1013 bits. This equates to only 0.72 hours using an OC-192c/STM-64c payload rather than 55.6 hours using an STS-3c/VC-4 bulk filled payload (149.76 Mb/s).The graph in Figure plots test time versus residual BER and shows the difference in test time for OC-192c/STM-64c payloads versus an OC-48c/STM-16c payload.The graphs are plotted for different confidence limits and they clearly indicate that the payload capacity is the dominant factor in improving the test time and not the confidence limit. Table 1 shows the exact test times for each BER threshold and confidence limit.
collected from::Product Note-OmniBER
