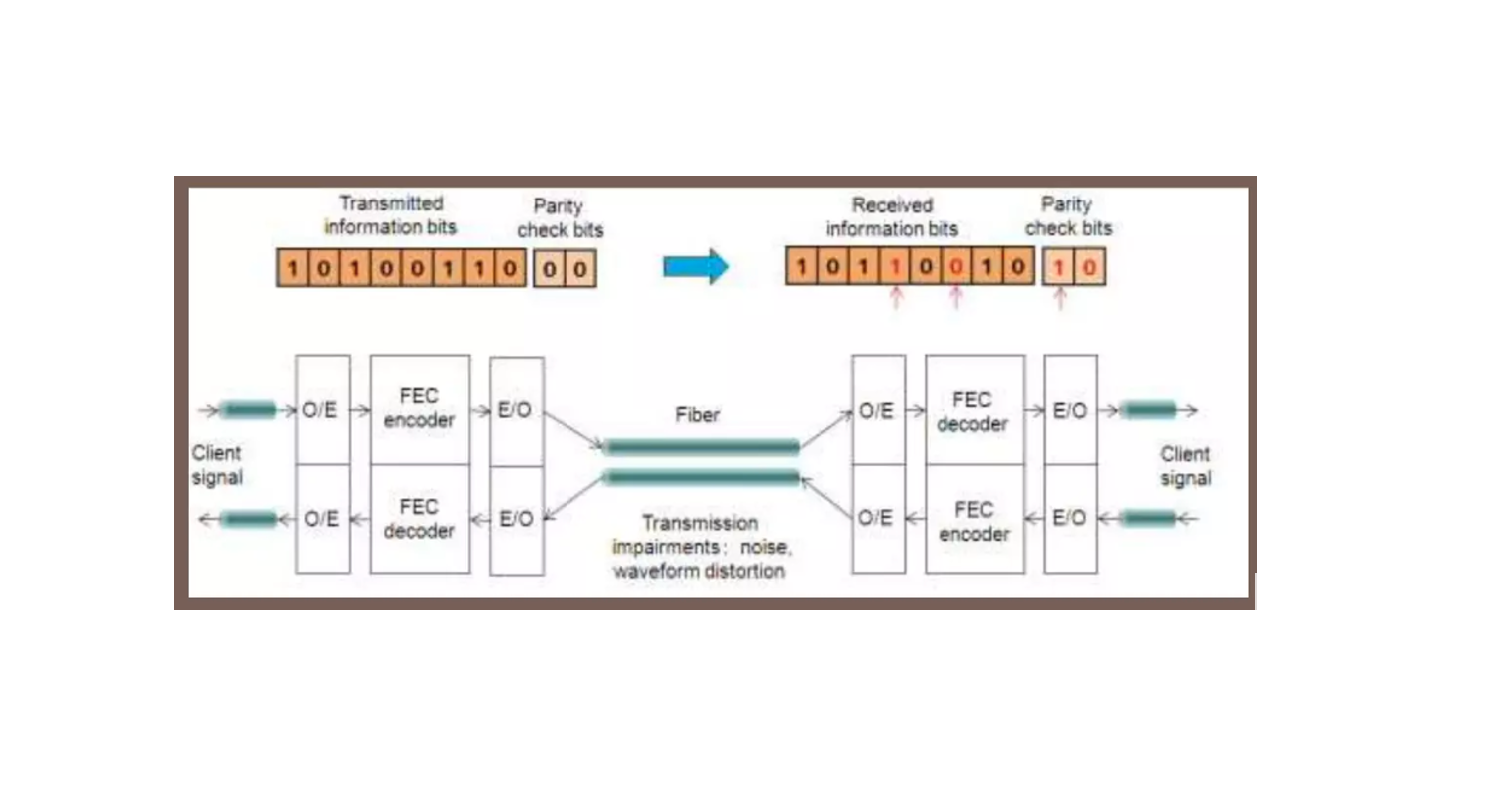
FEC codes in optical communications are based on a class of codes know as Reed-Solomon.
A Reed-Solomon code is specified as RS (n, k), which means that the encoder takes k data bytes and adds parity bytes to make an n bytes codeword. A Reed-Solomon decoder can correct up to t bytes in the codeword, where 2t=n – k.
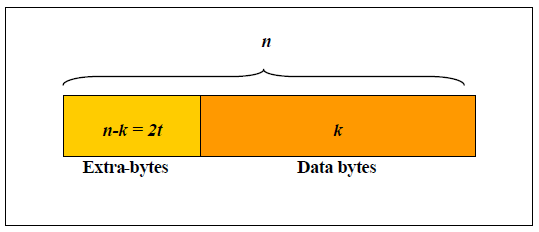
ITU recommendation G.975 proposes a Reed-Solomon (255, 239). In this case 16 extra bytes are appended to 239 information-bearing bytes. The bit rate increase is about 7% [(255-239)/239 = 0.066], the code can correct up to 8 byte errors [255-239/2 =8] and the coding gain can be demonstrated to be about 6dB.
The same Reed-Solomon coding (RS (255,239)) is recommended in ITU-T G.709. The coding overhead is again about 7% for a 6dB coding gain. Both G.975 and G.709 improve the efficiency of the Reed-Solomon by interleaving data from different codewords. The interleaving technique carries an advantage for burst errors, because the errors can be shared across many different codewords. In the interleaving approach lies the main difference between G.709 and G.975: G.709 interleave approach is fully standardized,while G.975 is not.
The actual G.975 data overhead includes also one bit for framing overhead, therefore the bit rate exp ansion is [(255-238)/238 = 0.071]. In G.709 the frame overhead is higher than in G.975, hence an even higher bit rate expansion. One byte error occurs when 1 bit in a byte is wrong or when all the bits in a byte are wrong. Example: RS (255,239) can correct 8 byte errors. In the worst case, 8 bit errors may occur, each in a separate byte so that the decoder corrects 8 bit errors. In the best case, 8 complete byte errors occur so that the decoder corrects 8 x 8 bit errors.
There are other, more powerful and complex RS variants (like for example concatenating two RS codes) capable of Coding Gain 2 or 3 dB higher than the ITU-T FEC codes, but at the expense of an increased bit rate (sometimes as much as 25%).
FOR OTN FRAME: Calculation of RS( n,k) is as follows:-
*OPU1 payload rate= 2.488 Gbps (OC48/STM16)
*Add OPU1 and ODU1 16 bytes overhead:
3808/16 = 238, (3808+16)/16 = 239
ODU1 rate: 2.488 x 239/238** ~ 2.499Gbps
*Add FEC
OTU1 rate: ODU1 x 255/239 = 2.488 x 239/238 x 255/239
=2.488 x 255/238 ~2.667Gbps
NOTE:4080/16=(255)
**Multiplicative factor is just a simple math :eg. for ODU1/OPU1=3824/3808={(239*16)/(238*16)}
Here value of multiplication factor will give the number of times for rise in the frame size after adding header/overhead.
As we are using Reed Soloman(255,239) i.e we are dividing 4080bytes in sixteen frames (The forward error correction for the OTU-k uses 16-byte interleaved codecs using a Reed- Solomon S(255,239) code. The RS(255,239) code operates on byte symbols.).
Hence 4080/16=255…I have understood it you need to do simpler maths to understand..)
