noise figure
Amplified Spontaneous Emission (ASE) Noise in EDFA Systems Amplified Spontaneous Emission (ASE) Noise in EDFA Systems A comprehensive engineering reference...
-
Free
-
March 1, 2026
Optical Amplifier Noise Figure: Definitions, Calculations, and Design Impact Deep Dive — Optical Amplifiers Optical Amplifier Noise Figure Definitions, Calculations,...
-
Free
-
March 1, 2026
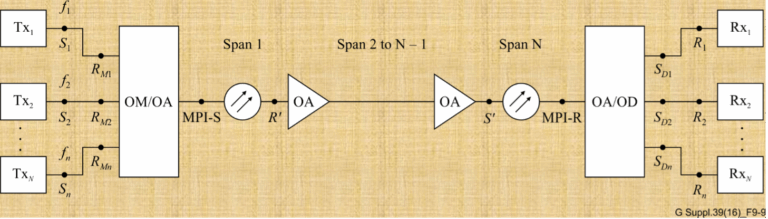
Based on my experience ,I have seen that Optical Engineers need to estimate Optical Signal-to-Noise Ratio (OSNR) often specially when...
-
Free
-
March 26, 2025
Optical networks are the backbone of the internet, carrying vast amounts of data over great distances at the speed of...
-
Free
-
March 26, 2025
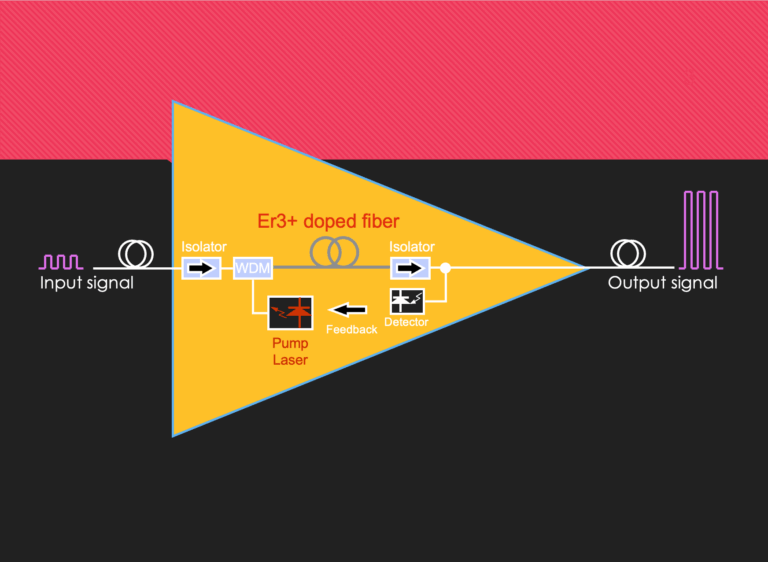
When working with amplifiers, grasping the concept of noise figure is essential. This article aims to elucidate noise figure, its...
-
Free
-
March 26, 2025
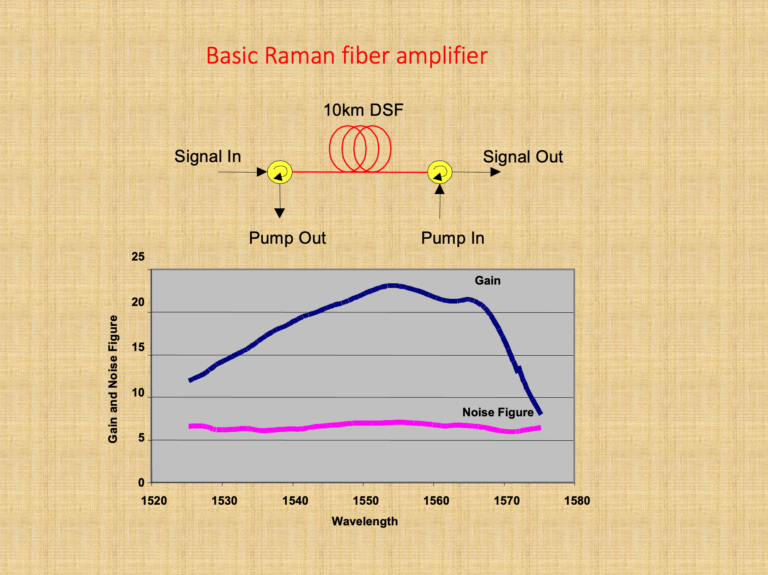
In the context of Raman amplifiers, the noise figure is typically not negative. However, when comparing Raman amplifiers to other...
-
Free
-
March 26, 2025
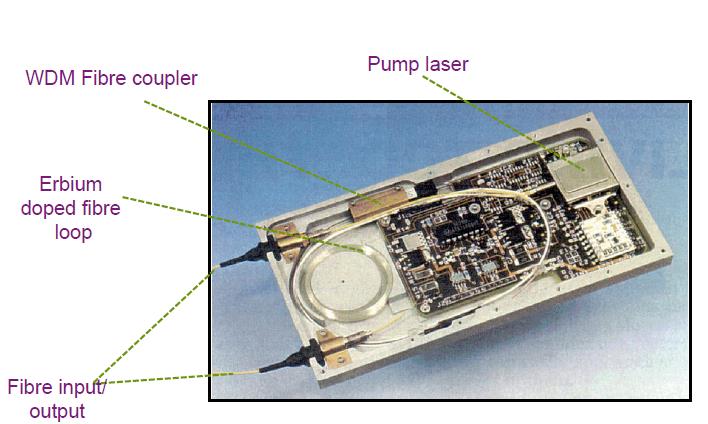
The main advantages and drawbacks of EDFAs are as follows. Advantages Commercially available in C band (1,530 to 1,565 nm)...
-
Free
-
March 26, 2025
The 980nm pump needs three energy level for radiation while 1480nm pumps can excite the ions directly to the metastable...
-
Free
-
March 26, 2025
Explore Articles
- Analysis
- Automation
- Careers and Learning Paths
- Coherent Optics
- Data Center Interconnect
- Free
- Fundamentals
- Management
- Network Architecture
- Planning & Design
- Premium
- Security
- Standards
- Submarine and Long-Haul
- Technical
- Testing
- Tools and Simulators
- Trends & News
- Troubleshooting and Operations
- Vendor and Product Landscape
Filter Articles
ResetTags
automation
ber
Coherent detection
coherent optical transmission
coherent optics
Data transmission
distributed Raman amplification
DWDM
edfa
EDFA noise figure
fec
Fiber optics
Fiber optic technology
Forward Error Correction
Latency
modulation
network automation
noise figure
optical
Optical communication
Optical fiber
Optical network
optical network automation
Optical network design
optical networking
Optical networks
Optical signal-to-noise ratio
Optical transport network
OSNR
OSNR calculation
OTN
Probabilistic Constellation Shaping
Q-factor
raman
Raman Amplifier
ROADM
Signal integrity
Signal quality
Slider
spectral efficiency
submarine
Submarine Cable
submarine cable systems
Telecommunications
Ticker