Network performance
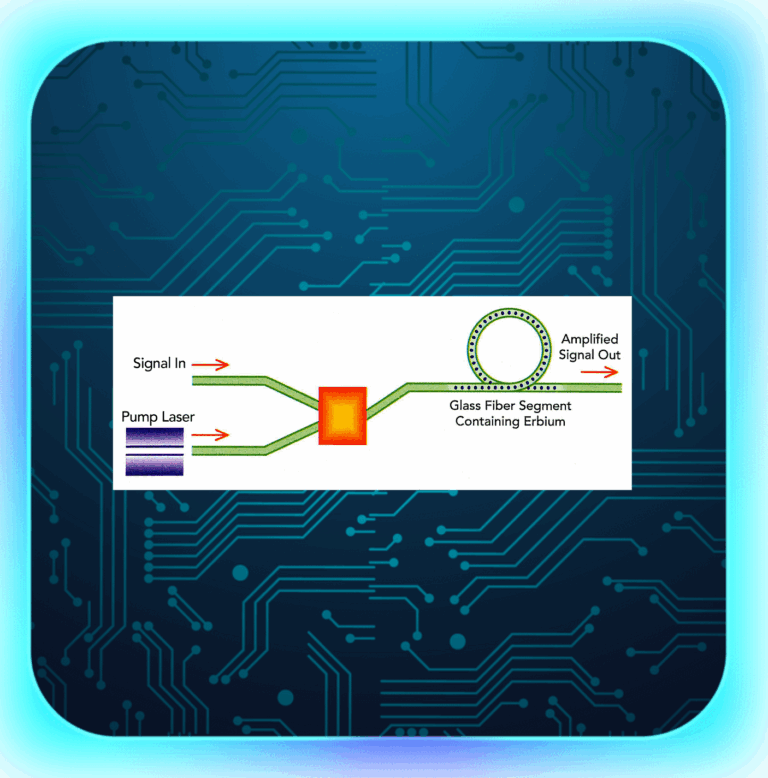
Optical Amplifiers (OAs) are key parts of today’s communication world. They help send data under the sea, land and even...
-
Free
-
March 26, 2025
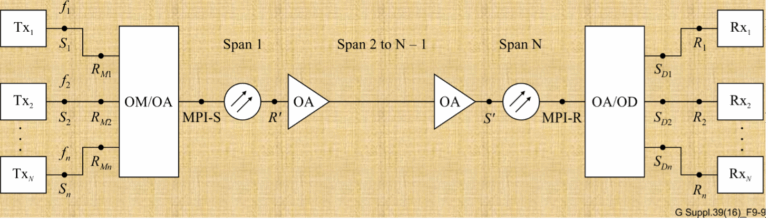
Optical networks are the backbone of the internet, carrying vast amounts of data over great distances at the speed of...
-
Free
-
March 26, 2025
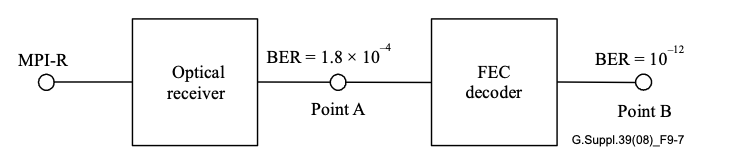
Forward Error Correction (FEC) has become an indispensable tool in modern optical communication, enhancing signal integrity and extending transmission distances....
-
Free
-
March 26, 2025
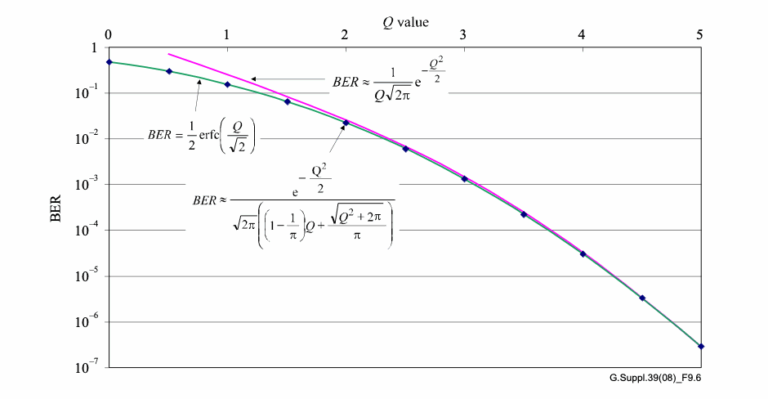
Signal integrity is the cornerstone of effective fiber optic communication. In this sphere, two metrics stand paramount: Bit Error Ratio...
-
Free
-
March 26, 2025
The ITU standards define a “suspect internal flag” which should indicate if the data contained within a register is ‘suspect’...
-
Free
-
March 26, 2025
Explore Articles
- Analysis
- Automation
- Careers and Learning Paths
- Coherent Optics
- Data Center Interconnect
- Free
- Fundamentals
- Management
- Network Architecture
- Planning & Design
- Premium
- Professional Development
- Security
- Standards
- Submarine and Long-Haul
- Technical
- Testing
- Tools and Simulators
- Trends & News
- Troubleshooting and Operations
- Vendor and Product Landscape
Filter Articles
ResetTags
400ZR
800ZR
automation
behavioral
ber
career
Chromatic Dispersion
COHERENT
coherent optical transmission
coherent optics
data center interconnect
Dispersion
DWDM
edfa
EDFA noise figure
fec
Fiber optic technology
gNMI
GSNR
hiring
Interview
launch power
Link Budget
NETCONF
network automation
noise figure
openconfig
optical
Optical communication
Optical fiber
Optical network
optical network automation
Optical signal-to-noise ratio
OSNR
OTN
Probabilistic Constellation Shaping
Q-factor
raman
ROADM
Slider
span loss
spectral efficiency
telemetry
Transponder
WSS