Signal quality
Optical networks are the backbone of the internet, carrying vast amounts of data over great distances at the speed of...
-
Free
-
March 26, 2025
Understanding Q-Factor in Optical Communications Understanding Q-Factor in Optical Communications Signal Quality Metrics and BER Relationship What is Q-Factor? Q...
-
Free
-
March 26, 2025
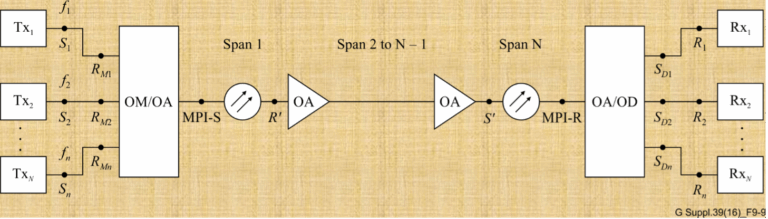
In a non-coherent WDM system, each optical channel on the line side uses only one binary channel to carry service information. The service transmission...
-
Free
-
March 26, 2025
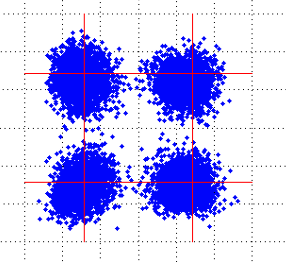
For coherent signals with wide optical spectrum, the traditional scanning method using an OSA or inband polarization method (EXFO) cannot...
-
Free
-
March 26, 2025
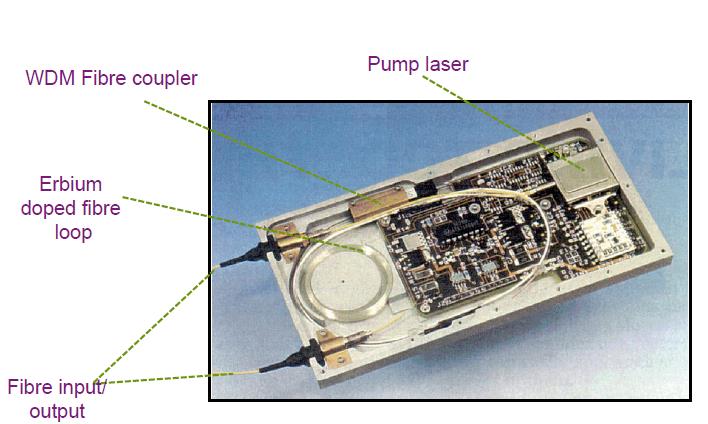
The main advantages and drawbacks of EDFAs are as follows. Advantages Commercially available in C band (1,530 to 1,565 nm)...
-
Free
-
March 26, 2025
Optical power tolerance: It refers to the tolerable limit of input optical power, which is the range from sensitivity to...
-
Free
-
March 26, 2025
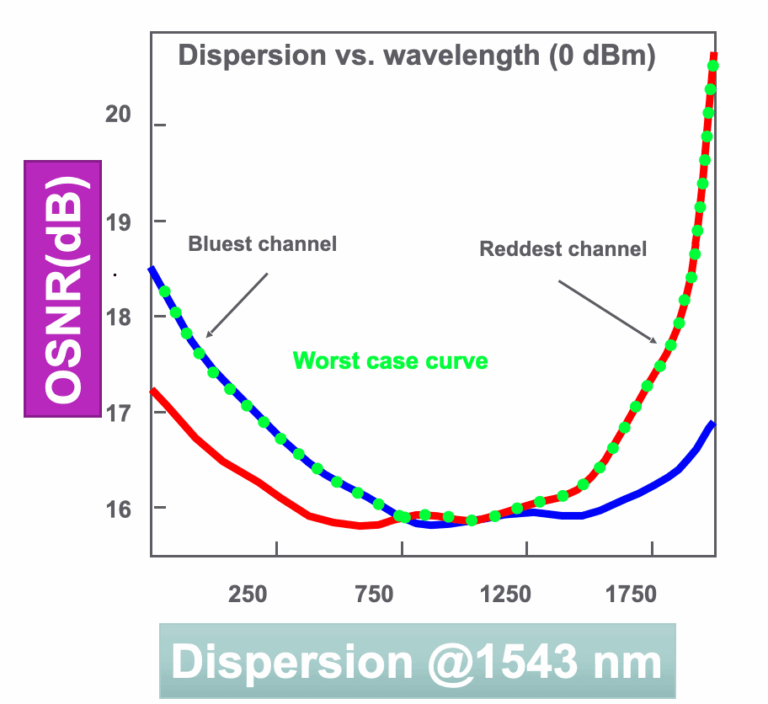
When the bit error occurs to the system, generally the OSNR at the transmit end is well and the fault...
-
Free
-
March 26, 2025
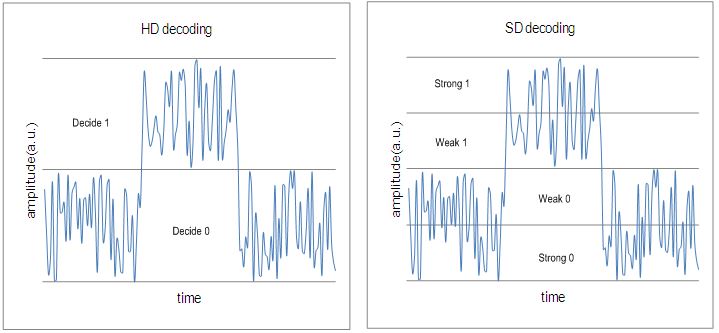
Items HD-FEC SD-FEC Definition Decoding based on hard-bits(the output is quantized only to two levels) is called the “HD(hard-decision) decoding”,...
-
Free
-
March 26, 2025
Explore Articles
- Analysis
- Automation
- Careers and Learning Paths
- Coherent Optics
- Data Center Interconnect
- Free
- Fundamentals
- Management
- Network Architecture
- Planning & Design
- Premium
- Security
- Standards
- Submarine and Long-Haul
- Technical
- Testing
- Tools and Simulators
- Trends & News
- Troubleshooting and Operations
- Vendor and Product Landscape
Filter Articles
ResetTags
automation
ber
Coherent detection
coherent optical transmission
coherent optics
Data transmission
distributed Raman amplification
DWDM
edfa
EDFA noise figure
fec
Fiber optics
Fiber optic technology
Forward Error Correction
Latency
modulation
network automation
noise figure
optical
Optical communication
Optical fiber
Optical network
optical network automation
Optical network design
optical networking
Optical networks
Optical signal-to-noise ratio
Optical transport network
OSNR
OSNR calculation
OTN
Probabilistic Constellation Shaping
Q-factor
raman
Raman amplification
Raman Amplifier
ROADM
Signal integrity
Signal quality
Slider
spectral efficiency
submarine
submarine cable systems
Telecommunications
Ticker